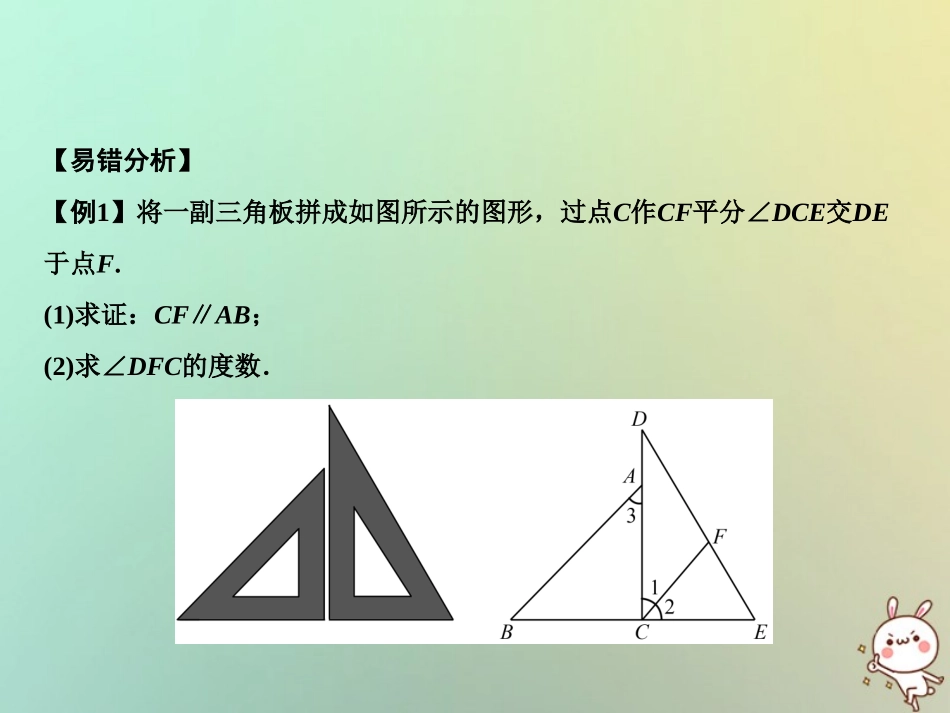
第七章平行线的证明章末小结2018秋季数学八年级上册•B【易错分析】【例1】将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;(2)利用三角形内角和定理进行计算即可.【解答】(1)∵CF平分∠DCE,∴∠1=∠2=12∠DCE,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB∥CF;(2)∵∠D=30°,∠1=45°,∴∠DFC=180°-30°-45°=105°.【例2】已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求证:∠P=90°.【分析】由AB∥CD,可知∠BEF与∠DFE互补,由角平分线的性质可得∠PEF+∠PFE=90°,由三角形内角和定理可得∠P=90°.【解答】∵AB∥CD,∴∠BEF+∠DFE=180°,又∵∠BEF的平分线与∠DFE的平分线相交于点P,∴∠PEF=12∠BEF,∠PFE=12∠DFE,∴∠PEF+∠PFE=12(∠BEF+∠DFE)=90°,∵∠PEF+∠PFE+∠P=180°,∴∠P=90°.【考点强化训练】命题与证明1.下列命题为假命题的是()A.三角形三个内角的和等于180°B.三角形两边之和大于第三边C.三角形两边的平方和等于第三边的平方D.三角形的面积等于一条边的长与该边上的高的乘积的一半C2.下列命题中:①锐角都相等;②大于直角且小于平角的角都是钝角;③互为相反数的两数的商是-1;④在同一平面内,若l1⊥l2,l1⊥l3则l3∥l2,其中真命题有()A.①②B.②③C.③④D.②④3.对于同一平面内的三条直线a、b、c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c;以其中两个论断作为条件,一个论断作为结论,组成你认为正确的因果关系的命题(用序号写出一个即可).D→③⑤②4.举反例说明下列命题是假命题.(1)如果a>b,那么|a|>|b|;解:a=1,b=-2,|a|<|b|;(2)a为实数,a+10的倒数为1a+10.解:a=-10时,1a+10无意义.5.如图,在直线AC上取一点O,作射线OB,已知OE、OF分别平分∠AOB、∠BOC.求证:OE⊥OF.证明:∵OE、OF分别平分∠AOB、∠BOC,∴∠BOE=12∠AOB,∠BOF=12∠BOC,∴∠BOE+∠BOF=12(∠AOB+∠BOC)=12×180°=90°,即OE⊥OF.平行线的性质与判定6.(桂林中考)如图,直线a、b被直线c所截,下列条件能判断a∥b的是()A.∠1=∠2B.∠1=∠4C.∠3+∠4=180°D.∠2=30°,∠4=35°B7.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为()A.10°B.20°C.25°D.30°8.如图,点E在AD的延长线上,下列条件中能判断BC∥AE的是()A.∠3=∠4B.∠A+∠ADC=180°C.∠1=∠2D.∠A=∠5CC9.如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数.解:∵∠1+∠2=180°,∠1+∠EFD=180°,∴∠2=∠EFD,∴EF∥AB,∠DEF=∠EDB,又∠DEF=∠A,∴∠EDB=∠A,∴DE∥AC,∴∠ACB=∠BED=60°.10.如图,已知∠1+∠2=180°,且∠3=∠4,试说明:DE∥AC.证明:∵∠1+∠2=180°,而∠1+∠DGE=180°,∴∠2=∠DGE,∴AB∥EF,∴∠4=∠DEF,又∠3=∠4,∴∠3=∠DEF,∴DE∥AC.11.如图,GD⊥AC,∠AFE=∠ABC,∠1+∠2=180°,BE与AC是否垂直?请说明理由.解:BE⊥AC.理由是:∵∠AFE=∠ABC,∴EF∥CB,∴∠1=∠EBC,又∠1+∠2=180°,∴∠EBC+∠2=180°∴DG∥BE,∴∠BEA=∠GDA.又∵GD⊥AC,∴∠GDA=90°,∴∠BEA=90°,∴BE⊥AC.