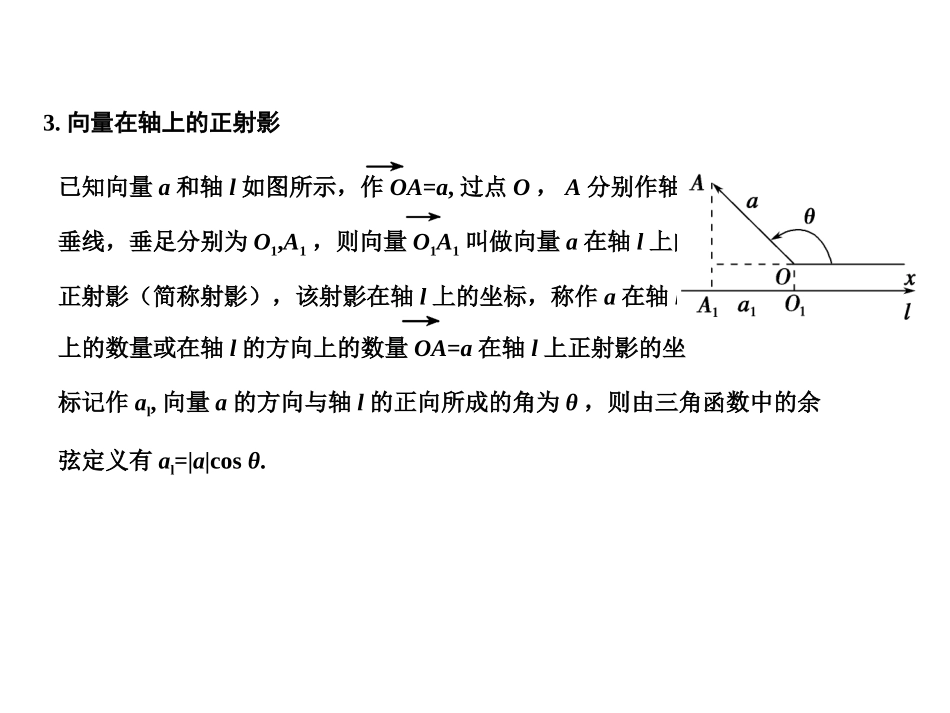
(理解平面向量数量积的含义及其物理意义/了解平面向量的数量积与向量投影的关系/掌握数量积的坐标表达式,会进行平面向量数量积的运算/能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系/会用向量方法解决某些简单的平面几何问题/会用向量方法解决简单的力学问题与其他一些实际问题)4.3平面向量的数量积及平面向量应用1.两个非零向量夹角的概念:已知非零向量a与b,作OA=a,OB=b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角,记作θ,
.注意:当θ=0时a与b同向;当θ=π时,a与b反向;当θ=时,a与b垂直,记a⊥b;2.平面向量数量积(内积)的定义:已知两个非零向量a与b,它们的夹角是θ,则数量|a||b|cosθ叫a与b的数量积,记作a·b,即有a·b=|a||b|·cosθ.3.向量在轴上的正射影已知向量a和轴l如图所示,作OA=a,过点O,A分别作轴l的垂线,垂足分别为O1,A1,则向量O1A1叫做向量a在轴l上的正射影(简称射影),该射影在轴l上的坐标,称作a在轴l上的数量或在轴l的方向上的数量OA=a在轴l上正射影的坐标记作al,向量a的方向与轴l的正向所成的角为θ,则由三角函数中的余弦定义有al=|a|cosθ.4.性质:两个非零向量a,b(1)a⊥b⇔a·b=0.(2)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a|·|b|.特别的a·a=|a|2或|a|=.(3)|a·b|≤|a||b|.5.运算律:a·b=b·a;(λa)·b=λ(a·b);(a+b)·c=a·c+b·c.1.已知|a|=2,|b|=4,a·b=-4,则a与b的夹角为()A.30°B.60°C.150°D.120°解析:答案:D2.若向量a=(1,2),b=(1,-3),则向量a与b的夹角等于()A.45°B.60°C.120°D.135°解析:答案:D3.两个非零向量a、b互相垂直,给出下列各式:①a·b=0;②a+b=a-b;③|a+b|=|a-b|;④|a|2+|b|2=(a+b)2;⑤(a+b)·(a-b)=0.其中正确的式子有()A.2个B.3个C.4个D.5个解析:①a·b=0,正确,②a+b与a-b方向不同,错误.③|a+b|2=|a|2+|b|2+2a·b=|a|2+|b|2,|a-b|2=|a|2+|b|2-2a·b=|a|2+|b|2,∴|a+b|=|a-b|.正确.④(a+b)2=|a|2+|b|2+2a·b=|a|2+|b|2.正确.⑤当|a|≠|b|时(a+b)·(a-b)=0不成立错误,故选B项.答案:B4.(2009·江苏卷)已知向量a和向量b的夹角为30°,|a|=2,|b|=,则向量a和向量b的数量积a·b=________.解析:a·b=|a||b|cosθ=2cos30°=3.答案:3向量的运算是指向量的加法、减法、实数与向量的积和向量的数量积等,向量的运算类似于实数的运算,要注意二者之间的联系和区别,有些问题从运算律到运算结果都非常类似,例如a2-b2=(a-b)·(a+b)等,同时要注意:①数形结合思想方法的运用;②向量加法、减法和数乘向量的结果是向量,而向量数量积的运算结果是实数.【例1】(1)证明:(a-b)2=a2-2a·b+b2;(2)设a、b是夹角为60°的单位向量,求①|2a+b|、|3a-2b|;②〈2a+b,3a-2b〉.解答:(1)证明:(a-b)2=(a-b)·(a-b)=(a-b)·a-(a-b)·b=a2-b·a-(a·b-b2)=a2-2a·b+b2.(2)① |2a+b|2=(2a+b)2=4a2+4a·b+b2=4+4|a||b|·cos60°+1=7,∴|2a+b|=.同理可求|3a-2b|=.②cos〈2a+b,3a-2b〉又0°≤〈2a+b,3a-2b≤〉180°,∴〈2a+b,3a-2b〉=60°.2.由于两个非零向量a=(x1,y1),b=(x2,y2),a,b的夹角为θ满足0°≤θ≤180°,所以用1.利用数量积求解长度问题是数量积的重要应用,要掌握此类问题的处理方法:【例2】已知a、b满足|a+b|=|a-b|,|a|=|b|=1,求|3a-2b|.解答:由|a+b|=|a-b|得,|a+b|2=3|a-b|2,即(a+b)2=3(a-b)2,∴a2+2a·b+b2=3(a2-2a·b+b2),∴8a·b=2a2+2b2=2|a|2+2|b|2=4,即a·b=,∴|3a-2b|=变式2.已知三个向量a、b、c两两所夹的角都为120°,|a|=1,|b|=2,|c|=3,求向量a+b+c与向量a的夹角.解答:由已知得(a+b+c)·a=a2+a·b+a·c=1+2cos120°+3cos120°=-,|a+b+c|==设向量a+b+c与向量a的夹角为θ,则cosθ即θ=150°,故向量a+b+c与向量a的夹角为150°.向量与其它知识结合,题目新颖而精巧,既符合考查知识的“交汇处”的命题要求,...