高二数学会考复习课件 圆锥曲线 课件VIP免费

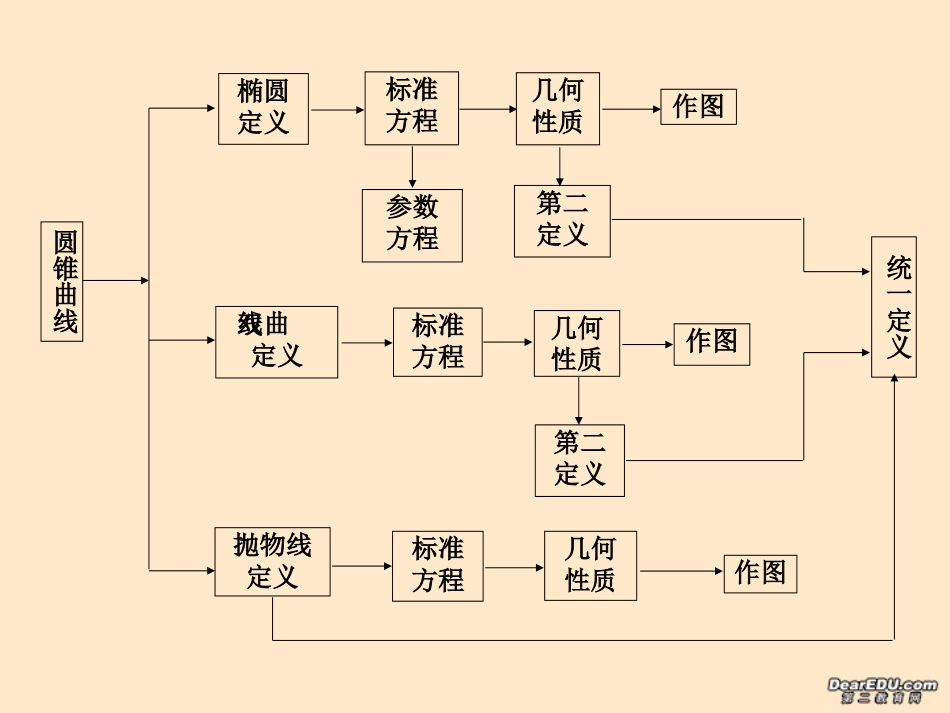
圆锥曲线椭圆定义双曲线定义标准方程几何性质作图参数方程第二定义标准方程几何性质作图第二定义几何性质作图标准方程抛物线定义统一定义1、掌握椭圆的定义，标准方程和椭圆的简单几何性质及椭圆的参数方程.2、掌握双曲线的定义、标准方程和双曲线的简单几何性质.3、掌握抛物线的定义、标准方程和抛物线的简单几何性质.4、能够根据具体条件利用各种不同的工具画椭圆、双曲线、抛物线的图形，了解它们在实际问题中的初步应用.考纲要求1.椭圆的定义:(1)椭圆的第一定义为：平面内与两个定点F1、F2的距离之和为常数(大于|F1F2|)的点的轨迹叫做椭圆.(2)椭圆的第二定义为：平面内到一定点F与到一定直线l的距离之比为一常数e(0＜e＜1)的点的轨迹叫做椭圆.1.双曲线的定义(1)双曲线的第一定义：平面内与两个定点F1、F2的距离差的绝对值是常数(小于|F1F2|)的点的轨迹叫做双曲线(2)双曲线的第二定义：平面内到一个定点F的距离和到一条定直线l的距离比是常数e(e＞1)的点的轨迹叫做双曲线2．双曲线标准方程的两种形式x2/a2-y2/b2=1,-x2/b2+y2/a2=1(a、b＞0)分别表示中心在原点、焦点在x轴、y轴上的双曲线1.抛物线的定义：平面内到定点F与到定直线l的距离之比为1的点的轨迹叫做抛物线2.抛物线标准方程的四种形式:y2=2px,y2=-2px,x2=2py,x2=-2py，(p＞0)分别表示焦点在x轴上，开口向右、开口向左，和焦点在y轴上，开口向上、开口向下的抛物线2、性质椭圆双曲线抛物线图形标准方程参数关系焦点坐标顶点坐标对称轴准线方程离心率渐近线)0(12222babyax)0,0(12222babyax)0(22ppxy)0,(a)0,0(x轴，长轴长2a；y轴，短轴长2bx轴，实轴长2a；y轴，虚轴长2bx轴)0,(c)0,(c)0,2(p10eace，1e1ecax2xaby2pxcax2OxyF1F2),0()0,(baOxyF1F2xyFo222bac222cba通径长度为2p3、统一性（1）从方程形式看:)0(12222babyax)0,0(12222babyax)0(22ppxy都属于二次曲线（2）从点的集合（或轨迹）的观点看：它们都是与定点和定直线距离的比是常数e的点的集合（或轨迹）（3）这三种曲线都是可以由平面截圆锥面得到的截线4、概念补遗：共轭双曲线、等轴双曲线、焦半径公式、椭圆的参数方程、焦点弦、有共同渐近线的双曲线系方程5、几个重要结论：设P是椭圆上的点，F1，F2是椭圆的焦点，∠F1PF2=θ,则1、当P为短轴端点时，SPF△1F2有最大值=bc2、当P为短轴端点时，∠F1PF2为最大3、椭圆上的点A1距F1最近，A2距F1最远4、过焦点的弦中，以垂直于长轴的弦为最短012222babyaxPB2B1F2A2A1F1x例1一动圆与x2+y2+6x+5=0外切，同时与圆x2+y2－6x－91=0内切，求动圆圆心的轨迹方程，并说明它是什么样的曲线。分析RO1O2yxOMNP|O1P|=R+2|O2P|=10－R|O1P|＋|O2P|=1212)3()3(2222yxyx(x+3)2+y2=4(x－3)2+y2=100本题可以按求点的轨迹方程的一般法（直译法）来求。设动圆圆心的坐标为(x，y)，利用初中学过的两圆相切的性质和判定定理列出方程，最后化简整理。(x，y)、两式的两边分别相加，得|O1P|＋|O2P|=1212)3()3(2222yxyxxyx12)3(22201084322yx1273622yx即分别将两已知圆的方程配方得(x+3)2+y2=4(x－3)2+y2=100由⊙P与⊙O1:(x+3)2+y2=4外切，得|O1P|=R+2由⊙P与⊙O2:(x－3)2+y2=100内切，得|O2P|=10－R解法1：设动圆圆心为P(x，y)，半径为R，两已知圆的圆心分别为O1、O2。如图，长分别为椭圆，它的长轴和短轴所以动圆圆心的轨迹是3612yxOMNRO1O2P(x，y)、两式的两边分别相加，得|O1P|＋|O2P|=121223ac，由上可得所以点P的轨迹是焦点为O1(－3，0）、O2(3，0)，长轴长等于12的椭圆，并且这个椭圆的中心与坐标原点重合>|O1O2|)0(12222babyaxP的轨迹方程为所以可设解法2：设动圆半径为R，两已知圆的圆心分别为O1、O2分别将两已知圆的方程配方得(x+3)2+y2=4(x－3)2+y2=100当⊙O1:(x+3)2+y2=4外切时，有|O1P|=R+2当⊙O2:(x－3)2+y2=100内切时，有|O2P|=10－RyxOMNRO1O2P(x，y)27936632bac，，1273622yx方程为于是得动圆圆心的轨迹。如图，长...