高二数学组合数的性质课件VIP免费

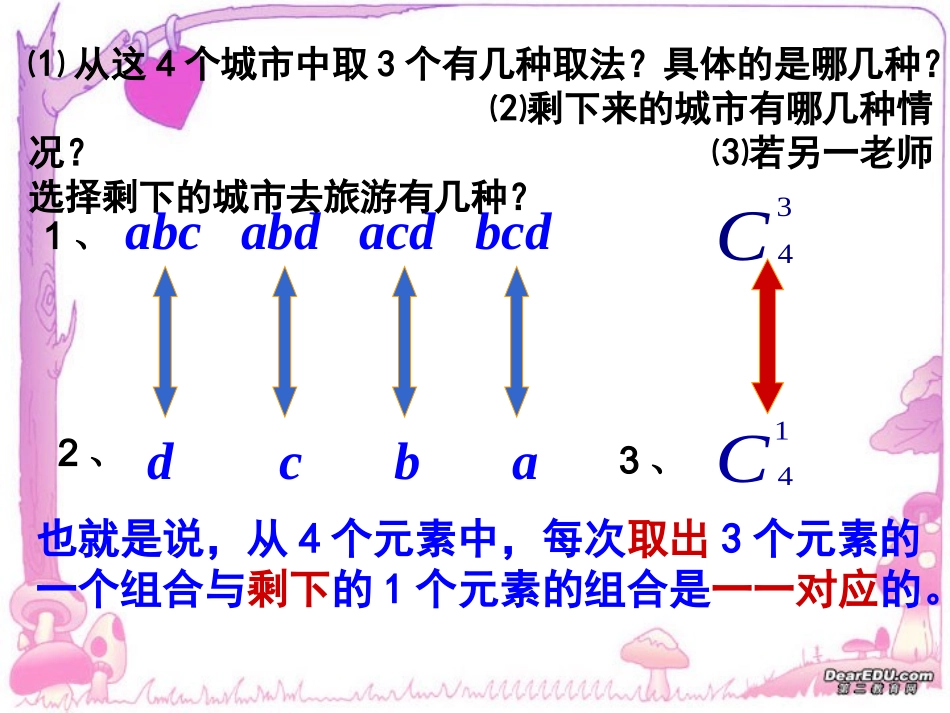
复习组合一般地，从n个不同元素中取出m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，用符号表示。mnCmmmnmnAAC!)1()2)(1(mmnnnn)!(!!mnmn五一将至，老师想去旅游，但不知道去哪儿好，大家能否介绍几个有名的旅游城市？abcabdacdbcddcba14C34C也就是说，从4个元素中，每次取出3个元素的一个组合与剩下的1个元素的组合是一一对应的。⑴从这4个城市中取3个有几种取法？具体的是哪几种？⑵剩下来的城市有哪几种情况？⑶若另一老师选择剩下的城市去旅游有几种？1、2、3、一般地，从n个不同的元素中取出m个元素后，剩下n-m个元素，因为从n个不同元素中取出m个元素的每一个组合，与剩下的n-m个元素的组合是一一对应的。所以从n个元素中取出m个元素的组合数等于从n个元素中取出n-m个元素的组合数即mnCnmnCmnmnnCC为了使公式在m=n时也成立，规定10nC小试身手1、计算①②③④1720C98100C3100C100100C归纳：,2NMMN当时利用这个公式可以使C计算简化思考归纳：从a,b,c,d,e,f这6个城市中选3个城市可以分两类一类含有a城市，另一类不含有a城市，因此，根据分类计数原理，上面的等式成立重新启航①我们从a,b,c,d,e,f这6个城市中选3个的选法，有几种？36C25C35C323655CCC②如果选中的3个城市中含有城市a的有几种选法？③如果选中的3个城市中不含有城市a的有几种选法？推广:从这n+1个不同的元素中，取出m个元素的组合数，这些组合可以分成两类：一类含，一类不含。含的组合是从这n个不同元素中取出m-1个元素的组合数为；不含的组合是从这n个不同的元素中取出m个元素的组合数为，再由加法原理，得1,2,1naaa1a1a1a2,3,1naaa1mnC1a2,3,1naaamnC1mnC11mmmnnnCCC性质2推广:从这n+1个不同的元素中，取出m个元素的组合数，这些组合可以分成两类：一类含，一类不含。含的组合是从这n个不同元素中取出m-1个元素的组合数为；不含的组合是从这n个不同的元素中取出m个元素的组合数为，再由加法原理，得1,2,1naaa1a1a1a2,3,1naaa1mnC1a2,3,1naaamnC1mnC11mmmnnnCCC性质2再试身手再试身手mnC1、化简（用形式表示）①90899999CC2、思考题：求证：01234555555552CCCCCC90100C10100C102004C9099C999C变式一：908910099CC变式三：10920052004cc变式二：7mC80mC81mC2、数学思想：mnmnnCC11mmmnnnCCC1、组合数的两个性质⑴从特殊到一般的归纳思想．⑵取法与剩法的一一对应的思想.(3)含与不含其元素的分类思想组合数的性质问题11.计算:310C710C从n个不同元素中取出m个不同的元素的方法从n个不同元素中取出n－m个不同的元素的方法一一对应２.用组合的定义思考mnCmnnC=性质1mnnmnCC你会证明吗?为了使公式在m=n时也成立，规定10nC问题2讨论：从n+1个不同的元素中取出m个元素的组合数设这n+1个不同元素为：13,2,1naaaa方法一：直接取方法二：分类取第一类：含有1a第二类：不含1a11mnmnmnCCC性质211mnmnmnCCC性质2)!1()!1(!)!(!!1mnmnmnmnCCmnmn)!1(!!)1(!mnmmnmnn)!1(!!)1(mnmnmmn!)1(!)!1(mnmnmnC1例题_______,.11056nnnCCC则若231010:.2xxCC解方程4104948474645)1(:.3CCCCCC求值394146352413)2(CCCCC13213210)1(32:.4nnnnnnnnnnnCnCCCKCCCCC化简已知