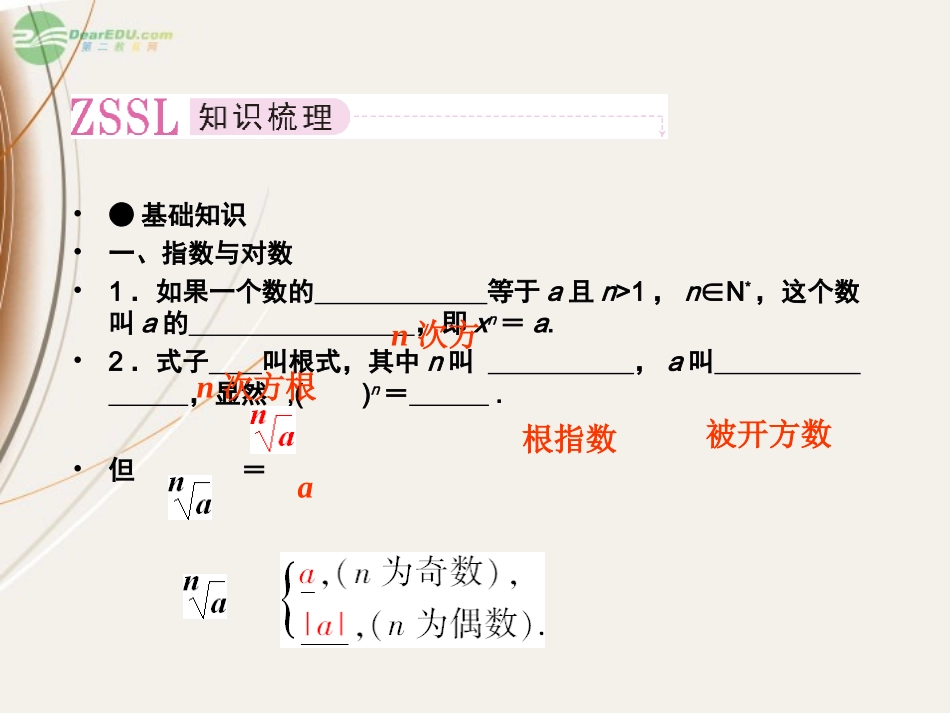
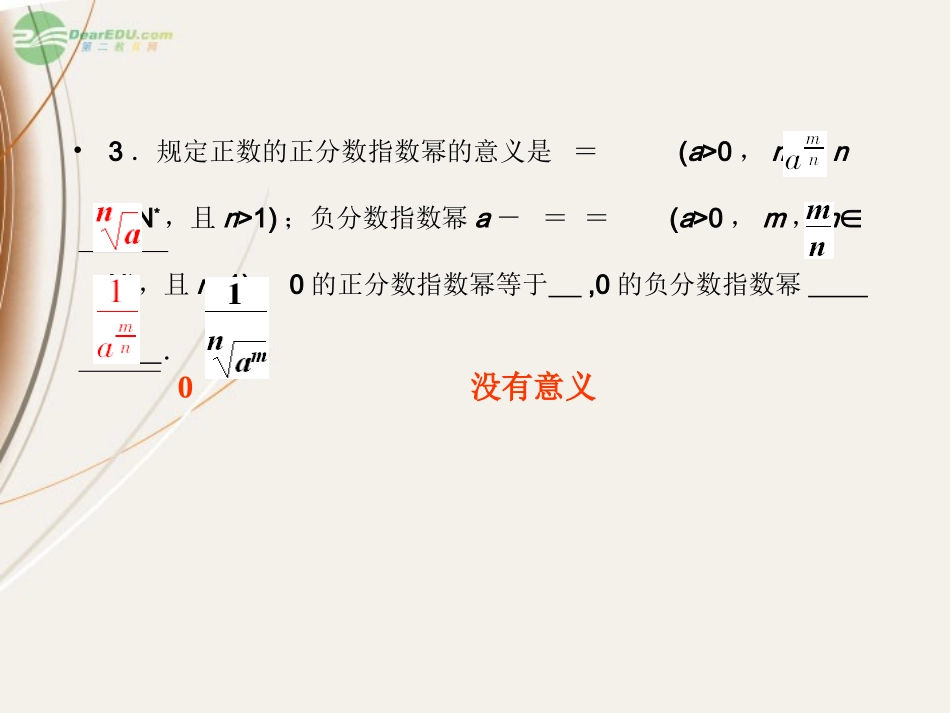
•●基础知识•一、指数与对数•1.如果一个数的等于a且n>1,nN∈*,这个数叫a的,即xn=a.•2.式子叫根式,其中n叫,a叫,显然,()n=.•但=n次方n次方根根指数被开方数a•3.规定正数的正分数指数幂的意义是=(a>0,m,nN∈*,且n>1);负分数指数幂a-==(a>0,m,n∈N*,且n>1);0的正分数指数幂等于,0的负分数指数幂.0没有意义•4.有理指数幂:①aras=(a>0,r,sQ)∈;②(ar)s=(a>0,r,sQ)∈;③(ab)r=(a>0,b>0,rQ)∈.•5.若ab=N,那么数b叫,记作logaN=b,其中a叫,N叫.即ab=N⇔•(a>0,且a≠1).和没有对数.(N>0)•6.N的常用对数记作,N的自然对数记作,它们分别以和为底.ar+sarsarbr以a为底N的对数对数的底数真数b=logaN负数零lgN1nN10e•7.alogaN=;loga1=;logaa=.•若a>0,a≠1,M>0,N>0,那么①loga(MN)=•;②loga=;③logaMn=(nR)∈N01logaM+logaNlogaM-logaNnlogaM•二、指数函数与对数函数•1.函数叫指数函数,其中x是自变量,a叫底数,函数叫对数函数,其中x是自变量,a叫底数.y=ax(a>0,且a≠1)y=logax(a>0且a≠1)•2.指数函数a>10
0,;x<0,.②x>0,;x<0,.(6)y=ax与y=()x=a-x关于对称(7)x轴是渐近线,即图象向左或向右无限接近x轴(8)a>1时,a越大,y=1上方的图象越接近轴(9)图象与直线x=1的交点(1,a)随着a增大而上升(0,+∞)(0,1)y>101y轴y对数函数a>101,;01,;01时,a越大,x=1右侧图象越接近轴(9)图象与直线y=1的交点(a,1)的横坐标,即为对数函数的底,a越大交点越向右(10)y=logax与y=ax互为反函数(0,+∞)(1,0)y>0y>0y<0y<0x轴x•●易错知识•一、运算法则运用错误•2.[(1-log63)2+log62·log618]÷log64=________.•答案:1•3.已知loga2=m,loga3=n,则a2m+n的值为________.•答案:12•二、没有分类出错•4.若实数a满足loga<1,则a的取值范围是________•答案:(0,)(1∪,+∞)•三、比较大小易混•5.如:将下列各数按从大到小的顺序排成一列•四、概念理解错误•6.设函数f(x)=logax(a>0,a≠1),若f(x1x2…x2009)=8,则的值等于()•A.4B.8•C.16D.2loga8•答案:C•失分警示:因对数运算法则不熟练而出错.•五、性质应用错误•7.设正数x、y满足log2(x+y+3)=log2x+log2y,则x+y的取值范围是()•A.(0,6]B.[6,+∞)•C.[1+,+∞)D.(0,1+]•答案:B•解析: log2(x+y+3)=log2x+log2y=log2xy,•∴x+y+3=xy,•由x、yR∈+知xy≤()2,∴x+y+3≤()2.•令x+y=A,∴A+3≤,•∴A≥6或A≤-2(舍去),故选B.•失分警示:本题不能分别求出x、y的值,只能将x+y看作一个参数来求解.•●回归教材•答案:D•答案:A•3.(课本P852题改编)函数y=的定义域是()•A.(3∞,+)B.[3∞,+)•C.(4∞,+)D.[4∞,+)•解析: log2x-2≥0⇒log2x≥2⇒x≥4.•答案:D•4.已知图中曲线C1、C2、C3、C4是函数y=logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为()•答案:B•6.(1)设y=a-x(a>0且a≠1),当a________∈时,y为减函数;此时当x________∈时,0<y<1.•(2)设y=loga(x+2)(a>0且a≠1)当a________∈时,y为减函数;此时当x________∈时,y<0.•答案:(1)(1∞,+)(0∞,+)(2)(0,1)(-1∞,+)•指数、对数式的化简和运算不独立命题,但在其他命题的研究中经常遇到等式的运算、变形、求值、化简及等式证明等.它是研究方程、不等式和函数的基础,很多数学问题的推理、判断也需要在等式的变形中解决.因此要熟练掌握并能灵活运用指数、对数的运算法则.•【例1】计算下列各式:•[总结评述]若式子中既有分数指数又有根式,可先把根式化成分数指数幂,再根据幂的运算性质进行计算;对数...