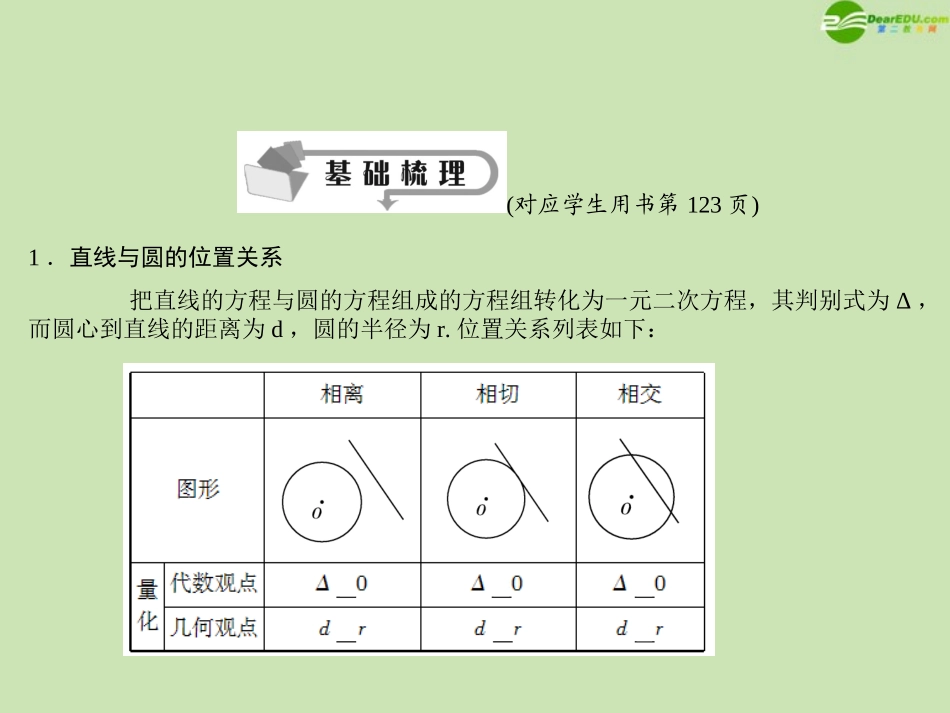
第4节直线与圆、圆与圆的位置关系(对应学生用书第123页)1.能判断直线与圆、圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题.3.初步了解用代数方法处理几何问题.(对应学生用书第123页)1.直线与圆的位置关系把直线的方程与圆的方程组成的方程组转化为一元二次方程,其判别式为Δ,而圆心到直线的距离为d,圆的半径为r.位置关系列表如下:①以圆x2+y2=r2上一点P(x0,y0)为切点的切线方程为:x0·x+y0·y=r2;②过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点为A、B,则切点弦AB方程为:x0x+y0y=r2.2.圆与圆的位置关系⊙O1、⊙O2半径分别为r1、r2,d=|O1O2|设两圆C1:x2+y2+D1x+E1y+F1=0(D12+E12-4F1>0)和C2:x2+y2+D2x+E2y+F2=0(D22+E22-4F2>0),则圆系方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1)①若令λ=-1,则(D1-D2)x+(E1-E2)y+F1-F2=0②其中(1)若C1和C2相交,则①式表示过两圆交点的圆,但不包括C2;②表示两圆的公共弦所在的直线方程.(2)若两圆相切,则②式表示内公切线方程.(3)若两圆相离,则②式表示两圆连心线C1C2的垂线的方程.3.弦长问题圆的弦长的计算:常用弦心距d,弦长一半12a及圆的半径r所构成的直角三角形来解,即r2=d2+(12a)2.若直线y=kx+b与曲线f(x,y)=0相交于点A(x1,y1),B(x2,y2),则所得弦长|AB|=1+k2|x1-x2|或|AB|=1+1k2|y1-y2|,因此,圆的弦长也可由以上公式求得.1.圆x2+y2-2x=0与x2+y2+4y=0的位置关系是(C)(A)相离(B)外切(C)相交(D)内切解析:圆的方程分别化为(x-1)2+y2=1,x2+(y+2)2=4, |O1O2|=1+4=5,而r1+r2=3,|r2-r1|=1,∴|r2-r1|<|O1O2|0)的公共弦的长为23,则a=______.解析:x2+y2+2ay=6,x2+y2=4,两式相减得y=1a.联立y=1a,x2+y2=4,消去y得x2=4a2-1a2(a>0).∴24a2-1a=23,解得a=1.答案:1(对应学生用书第123~125页)直线与圆的位置关系【例1】已知动直线l:y=kx+5和圆C:(x-1)2+y2=1,试问k为何值时,直线l与圆C相离、相切、相交.思路点拨:联立方程,消去一个未知数(如y),可得关于x的二次方程,再利用判别式Δ<0,Δ=0和Δ>0求k的取值范围.或者利用圆心到直线的距离与半径的大小关系,求参数k.解:法一:(代数法)联立方程y=kx+5,x-12+y2=1,消去y整理得(k2+1)x2+(10k-2)x+25=0,则Δ=(10k-2)2-4(k2+1)×25=-40k-96,∴当直线l与圆C相离时,有-40k-96<0,故k>-125;当直线l与圆C相切时,有-40k-96=0,故k=-125;当直线l与圆C相交时,有-40k-96>0,故k<-125.法二:(几何法)圆C:(x-1)2+y2=1的圆心为C(1,0),半径r=1.设直线l与圆心C的距离为d,则d=|k+5|k2+1.当d>r,即|k+5|k2+1>1,即k>-125时,直线l与圆C相离,当d=r,即|k+5|k2+1=1,即k=-125时,直线l与圆相切.当d<r,即|k+5|k2+1<1,即k<-125时,直线l与圆相交.直线和圆的位置关系的判定有两种方法:代数法与几何法.变式探究11:已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).(1)求证:不论m为何值,圆心在同一直线l上;(2)与l平行的直线中,哪些与圆分别相交、相切、相离?(1)证明:配方得(x-3m)2+[y-(m-1)]2=25.设圆心为(x,y),则x=3m,y=m-1,消去m得l:x-3y-3=0,故不论m...