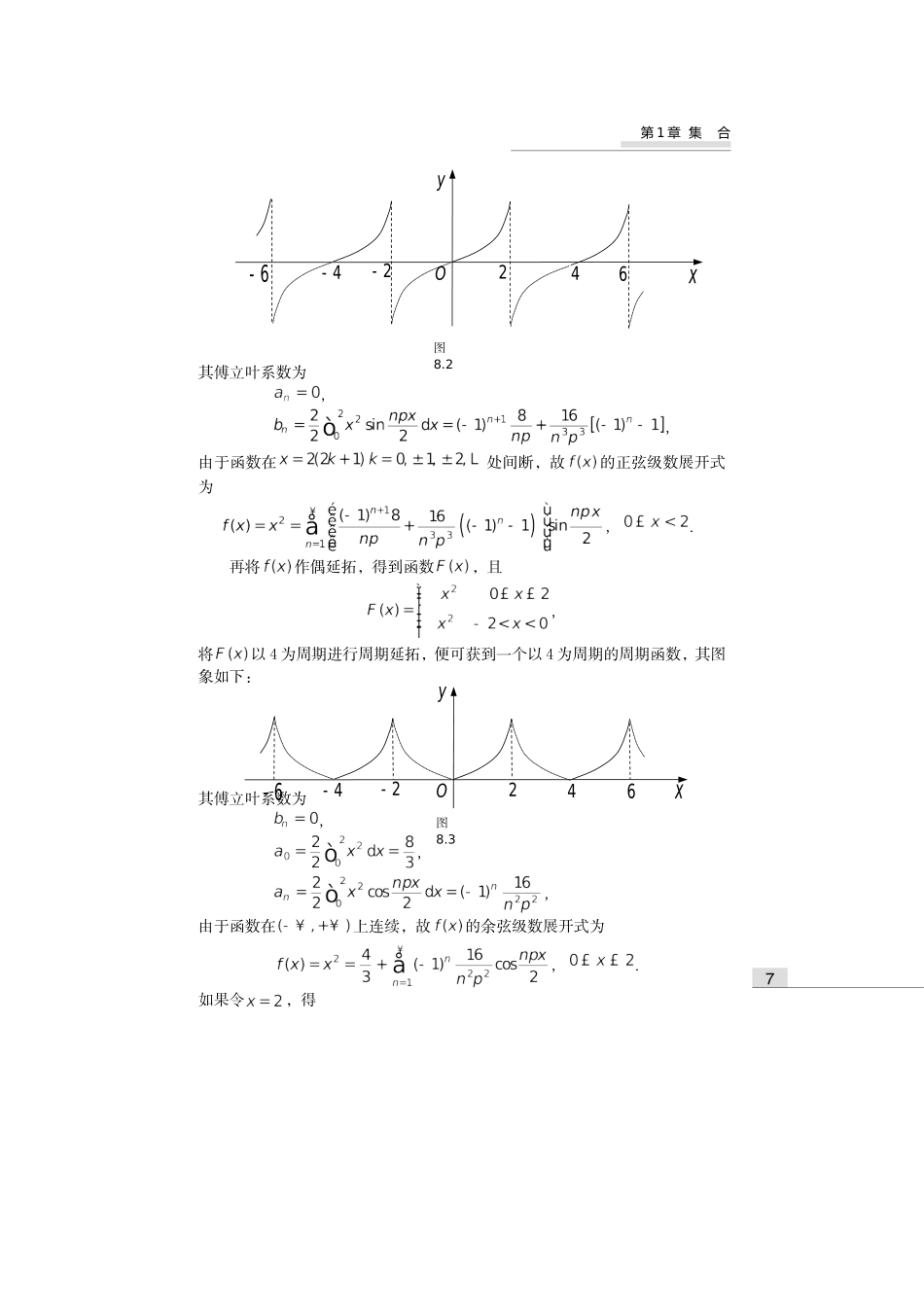
3第8节一般周期函数的傅里叶级数在第7节我们已经直接讲了一般周期为的周期函数的傅立叶级数。这节我们只需指出:(1)当时,周期函数的傅立叶级数就是周期函数的傅立叶级数;(2)如果是一般周期为的函数,作变量代换:或,就变成了周期为的函数把按周期展开成傅里叶级数,再代回,就得到周期函数的傅立叶级数。8离散数学【例8.1】设是周期为的周期函数,它在上的表达式为,将它展开成傅立叶级数.解。其傅立叶系数为,,.根据收敛定理,有,因此,的傅立叶展开式为的傅立叶级数展开式的和函数的图象如下:【例8.2】将函数展开成正弦级数和余弦级数.解。将作奇延拓,得到函数,且,再将以4为周期进行周期延拓,便可获到一个以4为周期的周期函数,其图象如图8.2所示:Oxy图8.112462-4-6-7第1章集合其傅立叶系数为,,由于函数在处间断,故的正弦级数展开式为,.再将作偶延拓,得到函数,且,将以4为周期进行周期延拓,便可获到一个以4为周期的周期函数,其图象如下:其傅立叶系数为,,,由于函数在上连续,故的余弦级数展开式为,.如果令,得Oxy图8.22462-4-6-Oxy图8.32462-4-6-8离散数学,即.对定义在任意区间上的函数,也可将它展开成傅立叶级数,其方法如下:作变量替换(黑板上一步步找此变换),即,当时,,将函数变成函数,可将按周期展开成傅立叶级数,再代回,就得到周期的傅里叶级数.【例8.3】将函数展开成傅立叶级数.解作变量替换,当时,则,而将以为周期进行周期延拓,可得到一个周期函数,其图象如下:其傅立叶系数为,,显然,点是函数的间断点,函数在其它点均连续,故的傅立叶展开式为.将代入上式,得周期的傅里叶级数Ot()Ftpp-图8.42p2p-3p3p-5-57第1章集合.习题13-8A类1.将下列周期函数(已给出函数在一个周期内的表达式)展开成傅立叶级数:(1);(2);(3);(4).2.将函数展开成正弦级数.3.将函数分别展开成正弦级数和余弦级数.B类1.将函数,()展成的傅立叶级数,并求级数的和.2.证明:在上有,并由此证明:.证要证等式右边是余弦级数。把偶延拓。傅里叶系数周期延拓后无间断点。所以在上有。令得。故。*3.将函数展开成傅立叶级数.