高二数学 9.6两个平面垂直的判定和性质课件 新人教版 课件VIP免费

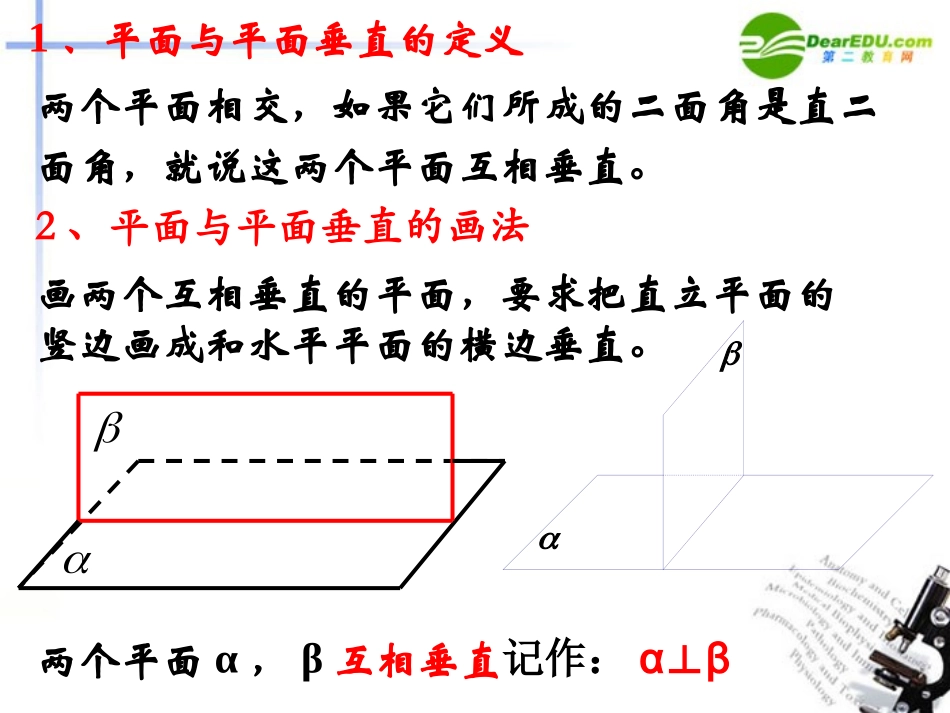
9.6两个平面垂直的判定和性质1．什么叫二面角的平面角？2．什么叫直二面角？3．我们是如何来定义两直线互相垂直的？.OABaOBaOAOBOAaO，．，．．)3)2)1a一．复习平面角是直角的二面角叫直二面角1、平面与平面垂直的定义两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直。两个平面α，β互相垂直记作：αβ⊥2、平面与平面垂直的画法画两个互相垂直的平面，要求把直立平面的竖边画成和水平平面的横边垂直。如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。②图形语言：ABβ⊥，ABααβ⊥。BA3、平面与平面垂直的判定定理：①文字语言：③符号语言：CDABECD设共面、知，由CDABABCDAB,BCDAB垂足为点,在平面内过点B作BE⊥CD，则∠ABE是二面角的平面角BEAB即二面角是直二面角CD4．平面与平面垂直的性质定理：①文字语言：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面；②图形语言：③符号语言：αβ,α∩β=⊥a，ABα，AB⊥a，且垂足为B，ABβ.⊥aBA已知：平面α⊥平面β，α∩β=CD，BAα，BA⊥CD，B为垂足，求证：BAβ.⊥CEDBA证明：在平面β内过点B作BE⊥CD，因为αβ⊥，所以BA⊥BE，又因为BA⊥CD，CD∩BE=B，所以BAβ⊥。aaaPP求证：（如图）已知：.,,,例2求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内。abβαcPβαabcP证明(同一法)：设α∩β＝c，过点P在平面α内作直线bc⊥，根据上面的定理有bβ⊥．因为经过一点只能有一条直线与平面β垂直，所以直线a应与直线b重合．性质推论例1、已知直线PA垂直正方形ABCD所在的平面，A为垂足。求证：平面PAC平面PBD。证明：。平面PBD平面PACBDC正方形ABCD中，ABDPA平面ABCDBD平面ABCDPA平面PACBD平面PBDBDABDPCO例2、空间四边形ABCD中，已知AB=3，AC=AD=2，∠DAC=BAC=BAD=60∠∠0，求证：平面BCD⊥平面ADCACBDO试说明理由有什么关系与平面直线问的中点分别是所在平面垂直于圆的直线过动点上的动点，是圆的直径，是圆：例?:.,,3VBCDEVAVCEDOVCCOCOABBCVOADE证明面面垂直的方法：1．定义：二面角为直二面角2．判定定理：aaABCDABCD，，，：性质定理性质AB)(1aaaPP.,,,2：性质