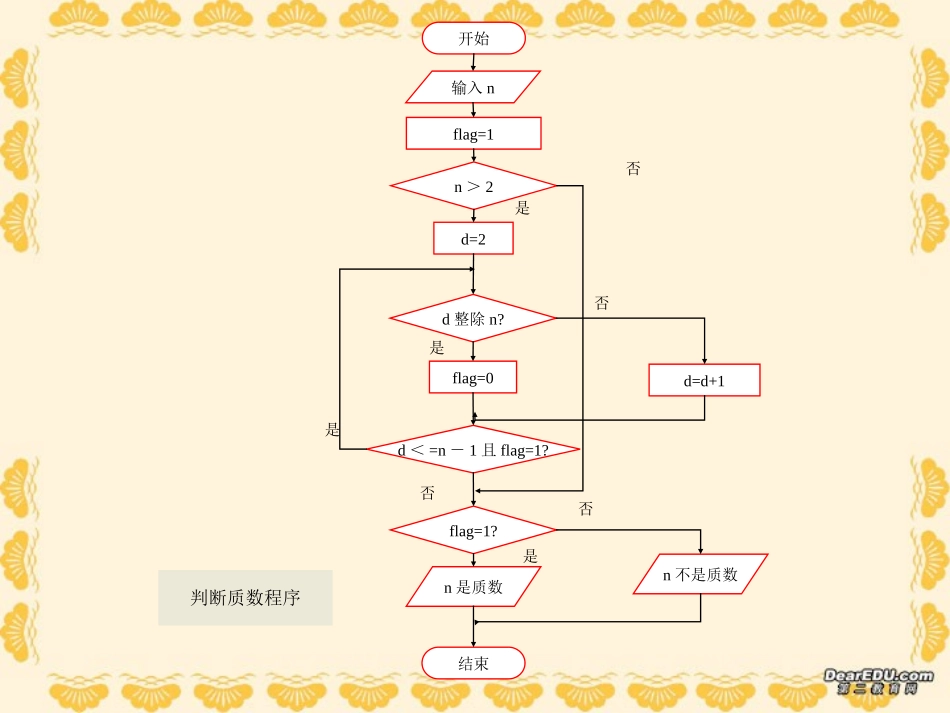
第一章算法初步1.1算法与程序框图1.2基本算法语句1.3算法案例1.1.2程序框图(流程图)算法分析:第一步:判断n是否等于2。若n=2,则n是质数;若n>2,则执行第二步。第二步:依次从2~(n-1)检验是不是n的因数,即整除n的数,若有这样的数,则n不是质数;若没有这样的数,则n是质数。例1、任意给定一个大于1的整数n,试设计出一个程序或步骤对n是否为质数做出判定算法可以用自然语言来描述,但为了使算法的程序或步骤表达得更直观,我们更常用图形方式来表示它。开始输入nflag=1d=2flag=0d=d+1n>2d整除n?d<=n-1且flag=1?flag=1?n是质数n不是质数结束是否否是否是否是判断质数程序顺序结构220x程序框图又称流程图,是一种规定的图形、指向线及文字说明来准确、直观地表示算法的图形。流程图的三种基本逻辑结构:条件结构循环结构顺序结构输入nflag=1条件结构flag=1?n是质数n不是质数结束是否循环结构flag=0d=d+1d整除n?d<=n-1且flag=1?否是否是p=(2+3+4)/2s=SQR(p*(p-2)*(p-3)*(p-4))输出s结束开始三角形面积计算(1)顺序结构的应用例3、已知一个三角形的三边长分别为2,3,4,利用海伦-秦九韶公式设计一个算法,求出它的面积,画出它的程序框图。开始输入a,b,ca+b>c,a+c>b,b+c>a是否同时成立?存在这样的三角形不存在这样的三角形结束否是判断三角形(2)条件结构的应用例4、任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出程序框图。开始sum=0i=i+1sum=sum+ii≤100?输出sum结束否是求和程序(3)循环结构的应用例5、设计一个计算1+2+3+…+100的值的算法,并画出程序框图。i=1开始输入aa≥0输出|a|=a输出|a|=-a结束NY求绝对值INPUT“输入一个实数a=”;aIFa≥0THENPRINT“|”;a;“|=”;aELSEPRINT“|”;a;“|=”;-aENDIFENDP.11练习1——求绝对值1、设计一个求任意数的绝对值的算法,并画出程序框图。算法步骤:第一步:输入任意一个实数a。第二步:判断输入的a是否大于0。若是,则直接输出a;若不是,则输出-a。算法分析:第一步:令f(x)=。因为f(1)<0,f(2)>0,所以设a=1,b=2。例2、用二分法设计一个求近似值,并画出程序框图。2abm第二步:令。判断f(m)是否为0。若是,则m为所求;若否,则继续判断f(a)·f(m)大于0还是小于0。23x220x第三步:若f(a)·f(b)>0,则令a=m;否则,令b=m。3第四步:判断︳a-b︳<0.005是否成立?若是,则a或b为满足条件的近似根;若否,则返回第二步。P.11练习2——二分法求平方根二分法求平方根P.11练习2——二分法求平方根开始a=1b=2f(x)=x2-3a=mb=mm=(a+b)/2a=mb=mf(m)=0f(x1)f(m)>0|a-b|<0.005结束输出所求的近似根mm=(a+b)/2ynnyny