高考数学 数列求和(第一课时)公开课课件VIP免费

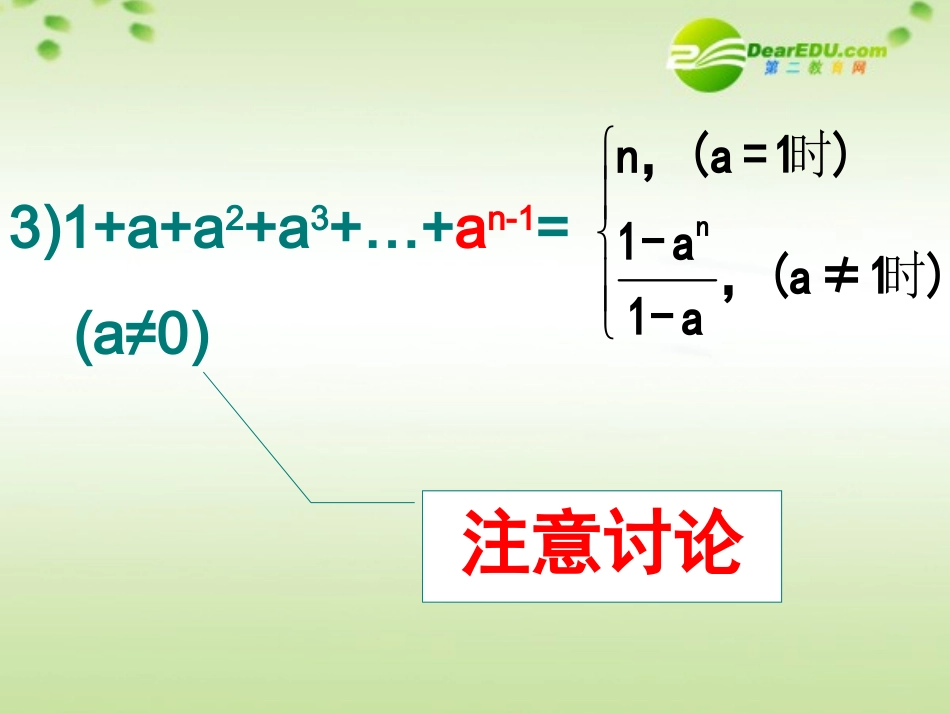
基础训练基础训练::246...2_________n1.1111..._________242n2.2nn122n3)1+a+a2+a3+…+an-1=(a≠0)注意讨论时时nn，(a=1)1-a，(a≠1)1-a复习复习::1.等差数列前n项和:2.等比数列前n项和:dnnnaaanSnn21211111111qqqaqnaSnnn数列{a}的前n项和12nnaaaS变式1······=(2+4+···+2n)···变式2：求和·········解：由题知······想一想想一想)12()12()12(2n分组求和即时总结：求前n项和关键的第一步：分析:数列特点：与首末等距离的两项之和等于首末两项之和。根据数列的特点，将其倒写后与原数列相加，以达到求和的目的。（联系：等差数列的前n项和推导过程以及高斯小时候巧解算术题）。例1倒序相加法函数)(xf对任意Rx都有21)1()(xfxf化简数列)1()1()2()1()0(fnnfnfnffan(1)例2求数列前n项的和,22,,26,24,2232nn分析如果一个数列的各项是由一个等差数列与一个等比数列对应项乘积组成，此时求和可采用错位相减法.错位相减法求数列前n项的和.解：由题可知，{}的通项是等差数列{2n}的通项与等比数列{}的通项之积设①②（设制错位）①－②得（错位相减）∴,22,,26,24,2232nnnn22n21nnnS222624223214322226242221nnnS1432222222222222)211(nnnnS1122212nnn1224nnnS求和求和分析：此数列为特殊数列，其通项的分母是两个因式之积，且两数相差1分析：此数列为特殊数列，其通项的分母是两个因式之积，且两数相差1)2)(1(1541431321Snnn若把通项作适当变形为，若把通项作适当变形为，2111)2)(1(1nnnn例3裂项相消解:解:111(1)(2)12nannnn11111111()()()()23344512nSnn11()22n2(2)nn求和求和)2)(1(1541431321Snnn解：由题知············变式1])1(1431321211[2nn12nn求)(,32114321132112111*Nnn。11nnan变式２：已知，若前n项和为10，则项数n为__________.na120例4：已知Sn=-1+3-5+7+…+(-1)n(2n-1),1)求S20,S212)求SnS20=-1+3+(-5)+7+……+（-37）+39S21=-1+3+(-5)+7+（-9）+……+39+（-41）=20=-21巩固练习1求和：nnxann11nx分析：通项等差数列，等比数列（错位相减）巩固练习2：已知函数13xxxf，数列na满足，11annafa1Nn（1）求证：数列na1是等差数列（2）记nnnaxaxaxxS221，求xSn（1）证明：由题意得131nnnaaannnnaaaa1313113111nnaa1nna1是等差数列（2）由（1）得23)1(311nnan通项nnnnnxnxaxb23等比数列，23n错位相减等差数列nnnxnxnxxxxS235374132xxSn①②1432233333)1(nnnxnxxxxxxSx1x当时当时2)13(2)231(23741)(nnnnnxSn1x112)23(1)1(3)()1(nnnxnxxxxxSx2212)1(2)13()23()(xxxxnxnxSnnn注意：首末两项相减；讨论系数不为0；注意代等比数列求和公式。①②1432235374nnxnxnxxx总的方向：1.转化为等差或等比数列的求和2.转化为能消项的情形思考方式：求和看通项（怎样的类型）若无通项，则须先求出通项方法及题型：1.等差、等比数列用公式法2.倒序相加法5.分组求和法4.裂项相消法3.错位相减法6.并项求和法点评：如果数列的通项公式可转化为)(1nfnf形式，常采用裂项求和的方法．特别地，当数列形如11nnaa，其中na是等差数列，可尝试采用此法．在什么情况下，用裂项求和？即时小结2.倒序...