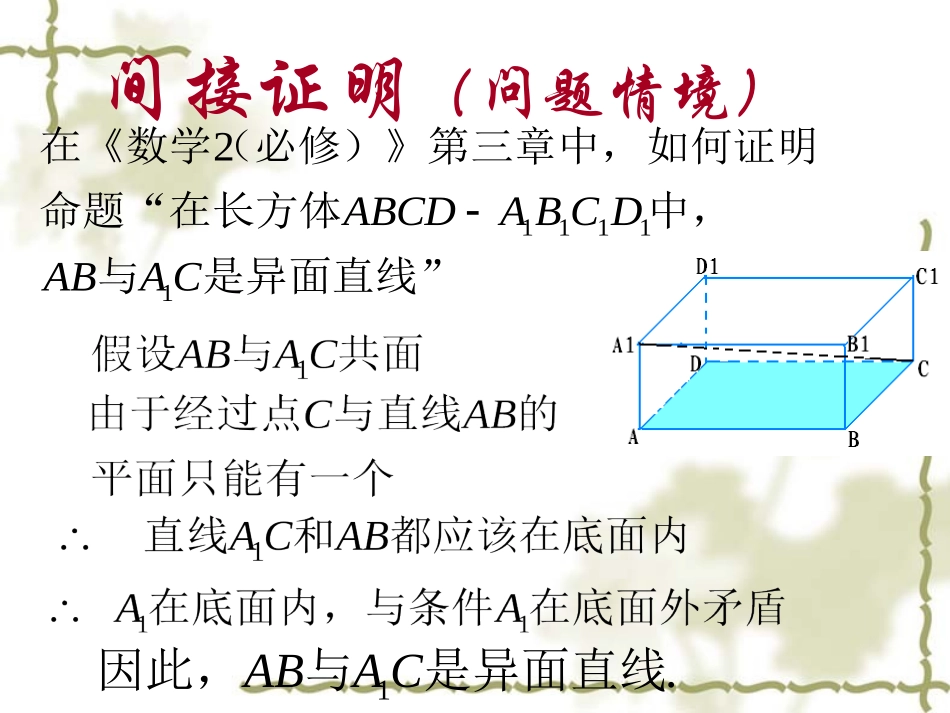
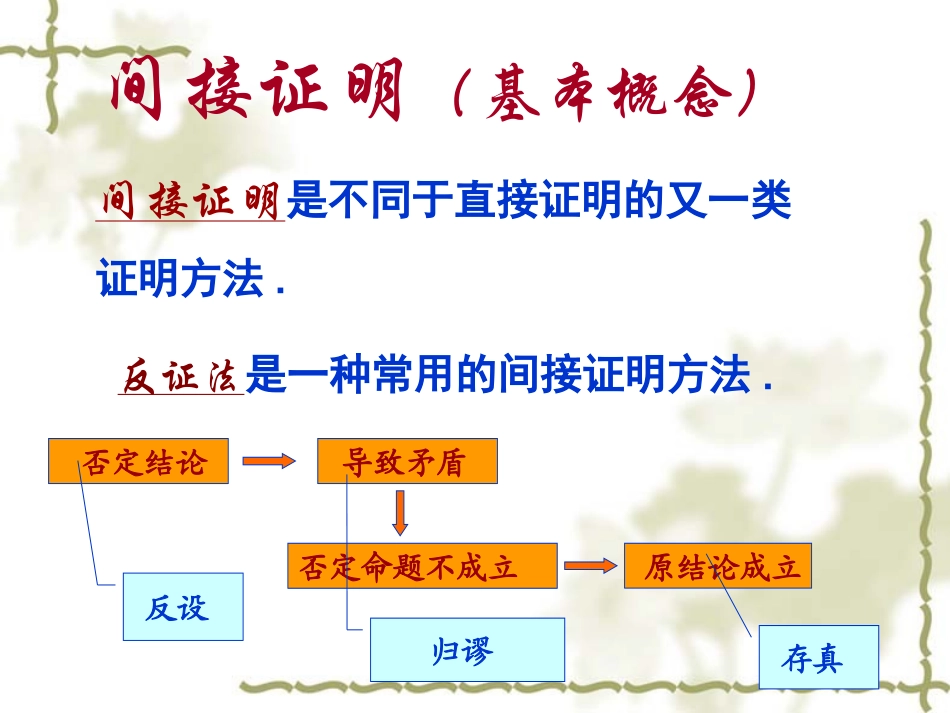
2.2.2间接证明间接证明(问题情境)是异面直线”与中,命题“在长方体如何证明(必修)》第三章中,在《数学CAABDCBAABCD111112.1是异面直线与因此,CAAB间接证明(基本概念)间接证明是不同于直接证明的又一类证明方法.反证法是一种常用的间接证明方法.否定结论导致矛盾否定命题不成立原结论成立反设归谬存真间接证明(基本概念)反证法的过程包括以下三个步骤:(1)反设——假设命题的结论不成立,即假定原命题的反面为真;(2)归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3)存真——由矛盾结果,断定反设不真,从而肯定原结论成立.间接证明(例题1).2小的正周期求证:正弦函数没有比先求出周期思路用反证法证明是最小正周期.2(例1)假设T是正弦函数的周期则对任意实数x都有:解xTxsin)sin(令x=0,得0sinT即.,ZkkTTT故假设最小正周期20从而对任意实数x都应有xxsin)sin(这与2sin)2sin(矛盾.因此,原命题成立..2小的正周期求证:正弦函数没有比间接证明(习题1)1.求证:若一个整数的平方是偶数,则这个数也是偶数.假设这个整数是奇数,可以设为2k+1,.Zk证:144)12(22kkk则有而)(Zkkk1442不是偶数这与原命题条件矛盾.(例题2).2不是有理数证明:.2,22.22)3()3(22),(2.22)2()2(21.0,,),1(22222222不是有理数互素矛盾,因此这与,约数的倍数,它们至少有公都是与则的倍数也是的倍数,所以是式表明,)式得代入(设的倍数也是的倍数,从而是式表明,)两边平方,变形得将(为互素的整数其中是有理数,可设假设qpqppplpNllqqqqpqqppq互素(回顾小结)间接证明反证法同一法枚举法