第一节 不等式的性质 课件VIP免费

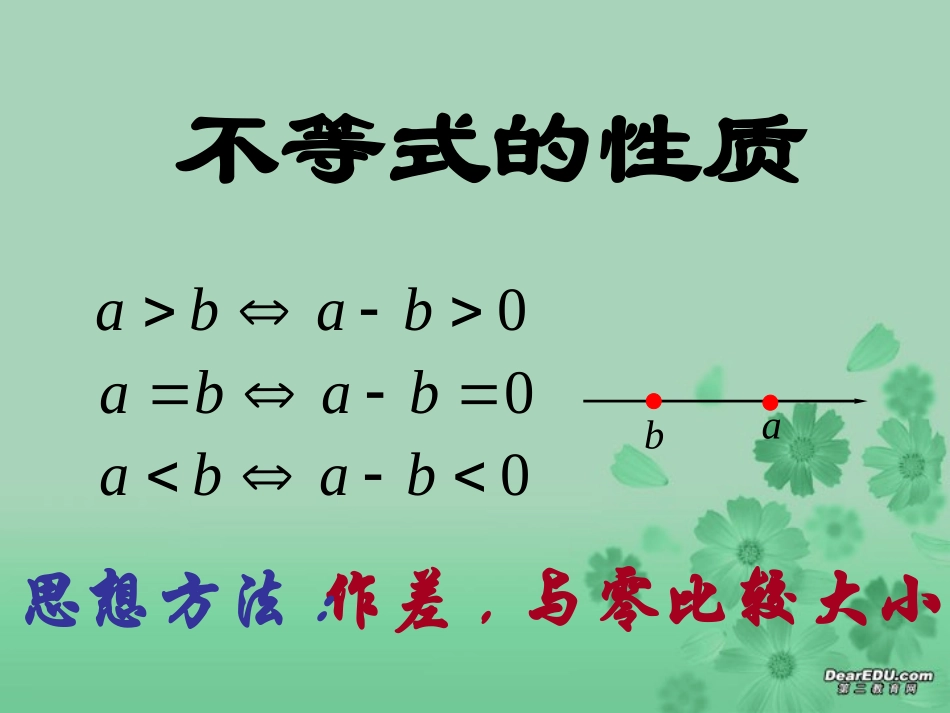
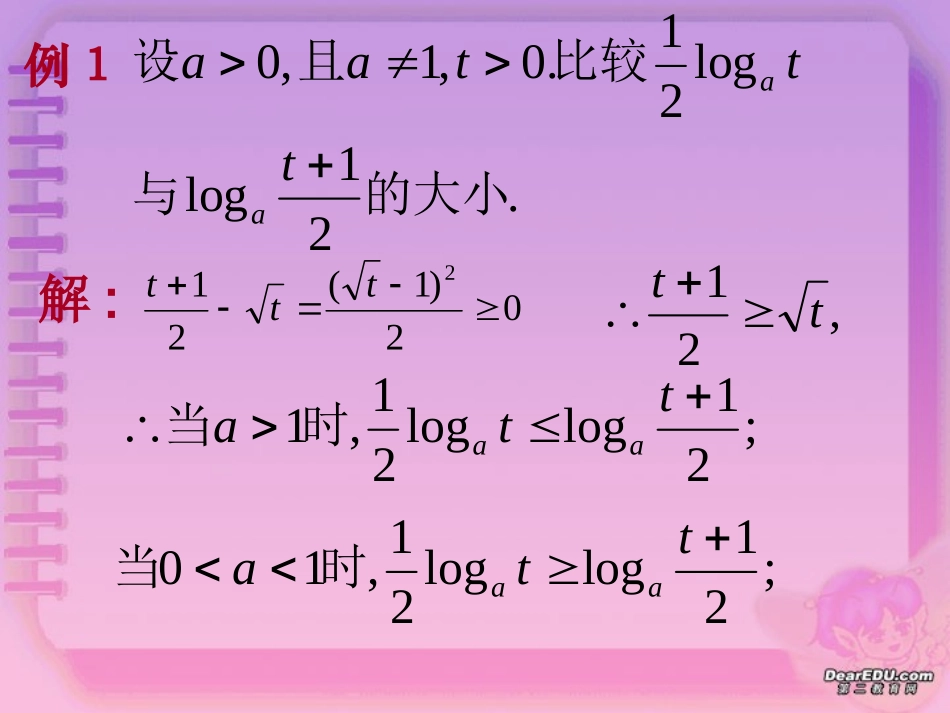不等式的性质ab0baba0baba0baba作差,与零比较大小思想方法:例1解:.21loglog21.0,1,0的大小与比较且设tttaaaa02)1(212ttt,21tt;21loglog21,1ttaaa时当;21loglog21,10ttaaa时当不等式性质定理1:.,;,baababba那么如果那么如果)(abba(对称性)证明:,ba,0ba由正数的相反数是负数,得,0)(ba)0(,0abba即.ab(充分性)不等式性质定理1:.,;,baababba那么如果那么如果)(abba(对称性)证明:,0abab由,0)(ab)0(,0baab或即.ba(必要性).abba不等式性质定理2:.,,cacbba那么且如果),(cacbba且(传递性)证明:,,cbba,0,0cbba根据两个正数的和仍是正数,得,0)()(cbba,0ca即.ca推论:.,cacbba且由不等式性质定理3:.,cbcaba那么如果)(cbcaba（加法单调性）证明:0)()(bacbcacbcabcabcbbacba)()(由性质定理3可以直接推得:不等式有可加性,可移项性.推论1:.,,dbcadcba那么且如果证明:dbcadbcbdccbcaba推论2:.,,dbcadcba那么且如果证明:相加法则badcdc.dbca相减法则同向可加性异向可减性不等式性质定理4:;,0,bcaccba那么且如果;,0,bcaccba那么且如果cbabcac)(证明:,0,baba,0)(,0cbac时当;bcac即,0)(,0cbac时当;bcac即同号得正异号得负推论1:.,0,0bdacdcba那么且如果推论2:0,(,1)nnababnNn如果那么且.,0,0dbcadcba那么且如果推论3:不等式性质定理5:0,(,1)nnababnNn如果那么且nnba假设证明:,0babann由ba这与矛盾,babann由ba这与矛盾.,nnnnbaba不成立假设例2.,0,0bcaccba求证已知证明:,0ba得不等式两边同乘以正数,1ab,11,11baab即,0c.bcac例2.,0,0bcaccba求证已知证明二:ababcbcac)(,0,0,0ababba,0,0bcacc.bcac.:,0,0,0dbecaeedcba求证已知000dbcadcba证明:dbca110dbecae,0e例3.)3(,5)2(1,1)1(4,)(42的取值范围求：已知函数例fffcaxxf的取值范围。件确定。最后运用已知条来表示与达式中，从而用的表然后再代入、设法表示与分析：利用)3()3()2()1()3()2()1(fffffcaff,)(2caxxf解：.)2(4)1(4)2()1(fcafcacafcaf即)]1(4)2([31)]1()2([31ffcffa解之得)1(35)2(389)3(ffcaf.340)2(38385)2(1,320)1(3535,1)1(4ffff，又20)3(1,20)1(35)2(381fff即把上述两式相加得：作业：P8习题6.1第6题再见再见