高考数学第一轮总复习3.3等比数列(第2课时)课件 文 (广西专版) 课件VIP免费

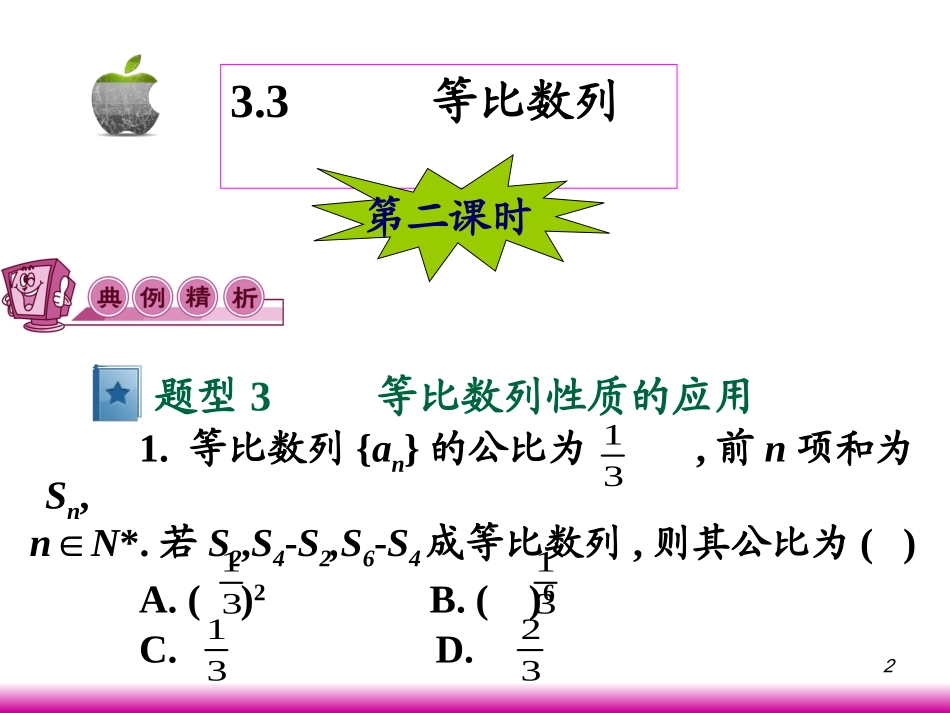
1第三章数列23.3等比数列第二课时题型3等比数列性质的应用1.等比数列{an}的公比为,前n项和为Sn,n∈N*.若S2,S4-S2,S6-S4成等比数列,则其公比为()A.()2B.()6C.D.13131313233解:设{an}的公比为q,首项为a1.由S2=a1+a1q,S4-S2=q2(a1+a1q),S6-S4=q4(a1+a1q),及S2,S4-S2,S6-S4成等比数列,可得其公比为q2=()2，故选A.点评：等比数列有着许多同构性质，如①{an}是等比数列，则{a2n}也是等比数列，{akn+b}也是等比数列；②Sn是等比数列{an}的前n项的和，若Sm≠0，则数列Sm，S2m-Sm，S3m-S2m，…成等比数列.134设正项等比数列{an}的首项a1=，前n项和为Sn，且210S30-(210+1)S20+S10=0，求数列{an}的通项公式.解：由已知得210(S30-S20)=S20-S10，即210·q10(S20-S10)=S20-S10.因为an＞0,所以S20-S10≠0,所以210·q10=1，所以q=.从而an=()n(n∈N*).拓展练习拓展练习12121252.已知等比数列{bn}与数列{an}满足bn=3an(n∈N*).(1)若a8+a13=m,求b1b2…b20;(2)若b3·b5=39,a4+a6=3,求b1b2…bn的最大值.解：(1)易证得{an}是以log3q为公差的等差数列(q为等比数列{bn}的公比).又a8+a13=m，所以b1b20=3a1·3a20=3a1+a20=3m，b2b19=3a2+a19=3m，b10b11=3a10+a11=3m，…所以b1b2…b20=(b1b20)10=310m.题型4等比数列与等差数列交汇6(2)由b3·b5=39，得a3+a5=9.又a4+a6=3，所以d=-3，a1=，所以于是所以，当n=5时，b1b2…bn取得最大值点评：等比数列是指数型函数，其指数的变化恰好是成等差数列变化的，即对一正项等比数列求对数后，就构成了一个新的等差数列.27227(-1)(-3).2nan13-2222121()(3)3(-10),nnnaannbbbbbnn7523.7已知等差数列{an},a2=9,a5=21.(1)求数列{an}的通项公式；(2)令bn=2an，求数列{bn}的前n项和Sn.解：(1)设数列{an}的公差为d.依题意得方程组解得所以数列{an}的通项公式为an=4n+1.(2)由an=4n+1，得bn=24n+1，所以数列{bn}是首项为b1=25,公比q=24的等比数列,于是得数列{bn}的前n项和拓展练习拓展练习119,421adad15.4ad54442(2-1)32(2-1).2-115nnnS83.已知数列{an}中，Sn是其前n项和，并且Sn+1=4an+2(n=1,2,…),a1=1.(1)设数列bn=an+1-2an(n=1,2,…)，求证：数列{bn}是等比数列；(2)设数列cn=(n=1,2,…)，求证：数列{cn}是等差数列；(3)求数列{an}的通项公式及前n项和.解：(1)证明：由Sn+1=4an+2,Sn+2=4an+1+2，两式相减，得Sn+2-Sn+1=4(an+1-an)，题型5等比数列中的探究性问题2nna9即an+2=4an+1-4an.(根据bn的构造，如何把该式表示成bn+1与bn的关系是证明的关键，注意加强恒等变形能力的训练.)所以an+2-2an+1=2(an+1-2an).又bn=an+1-2an，所以bn+1=2bn.①由S2=4a1+2，a1=1，得a1+a2=4a1+2，解得a2=5，则b1=a2-2a1=3.②由①和②知，数列{bn}是首项为3，公比为2的等比数列，故bn=3·2n-1.10(2)证明：因为所以又故数列{cn}是首项为，公差为的等差数列，所以(3)因为又所以所以当n≥2时，Sn=4an-1+2=2n-1(3n-4)+2；当n=1时，S1=a1=1也适合上式.综上可知,所求的前n项和为Sn=2n-1(3n-4)+2.(*),2nnnacnN-11111111-2323--.222224nnnnnnnnnnnnnaaaabcc111,22ac123431-.44ncn,2nnnac31-,44ncn31-,244nnan-2(3-1)2.nnan11点评：1.本例主要复习用等差、等比数列的定义证明一个数列为等差、等比数列，求数列的通项公式与前n项和.解决本题的关键在于由条件Sn+1=4an+2得出递推公式.2.解综合题要总览全局，尤其要注意上一问的结论可作为下面论证的已知条件，在后面求解的过程中适时应用.12已知数列{an}满足：a1=1，a2=2，且数列{anan+1}是公比为q的等比数列.设bn=a2n-1+a2n，数列{bn}的前n项和为Sn，试推断是否存在常数k，使对任意n∈N*都有Sn=2bn+k成立？若存在,求出k的值；若不存在,说明理由.解：由已知即所以数列a1，a3，a5，…，a2n-1，…和a2，a4，a6，…，a2n，…都是公比为q的等比数列.当q≠1时，拓展练习拓展练习121,nnnnaaqaa2,nnaqa13又bn=a1qn-1+a2qn-1=3qn-1，所以因为Sn=2bn+k，所以得q=2，所以当q=1时，a2n-1=1，a2n=2，从而bn=3，Sn=3n，不满足题设条件，故k=-3为所求.3(1-)33.1--11-nnnqbqSbqqq2,-1qq33-3.1-1-2kq141.在等比数列中，每隔相同的项抽出来的项按照原来的顺序排列，构成的新数列仍然是等比数列.2.一个等比数列的奇数项，仍组成一个等比数列，它的公比是原数列公比的二次幂.3.若{an},{bn}为等比数列,则{λan}(λ≠0),{|an|}，{}，{an2}，{manbn}(m≠0)仍为等比数列.4.解题时，应注意等比数列性质的应用，以减少运算量而提高解题速度.1na