高考数学第一轮总复习9.6空间向量的坐标运算(第2课时)课件 文 (广西专版) 课件VIP免费

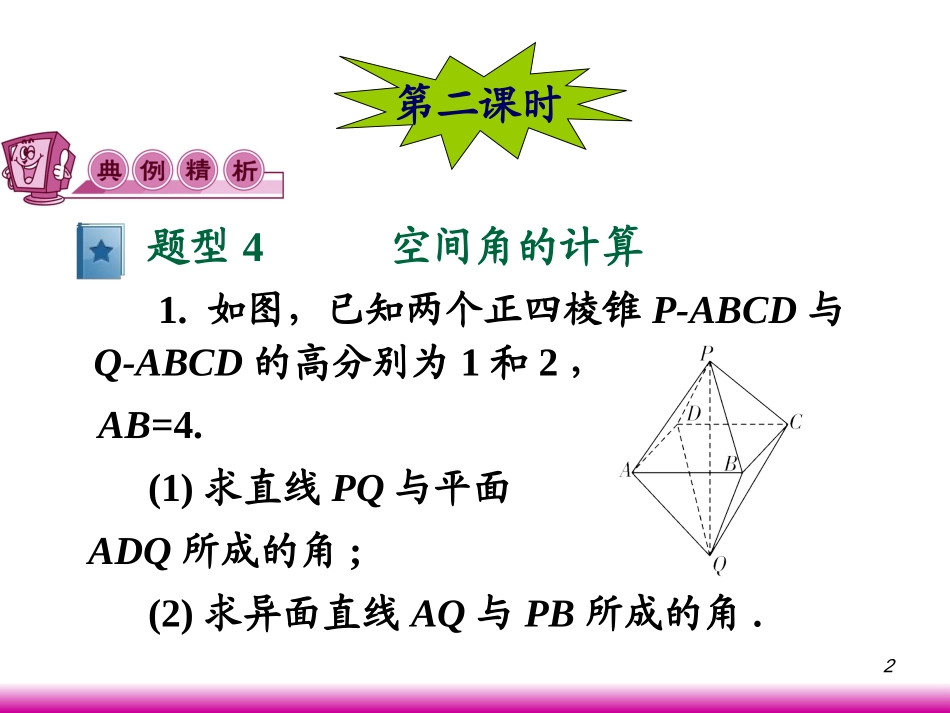
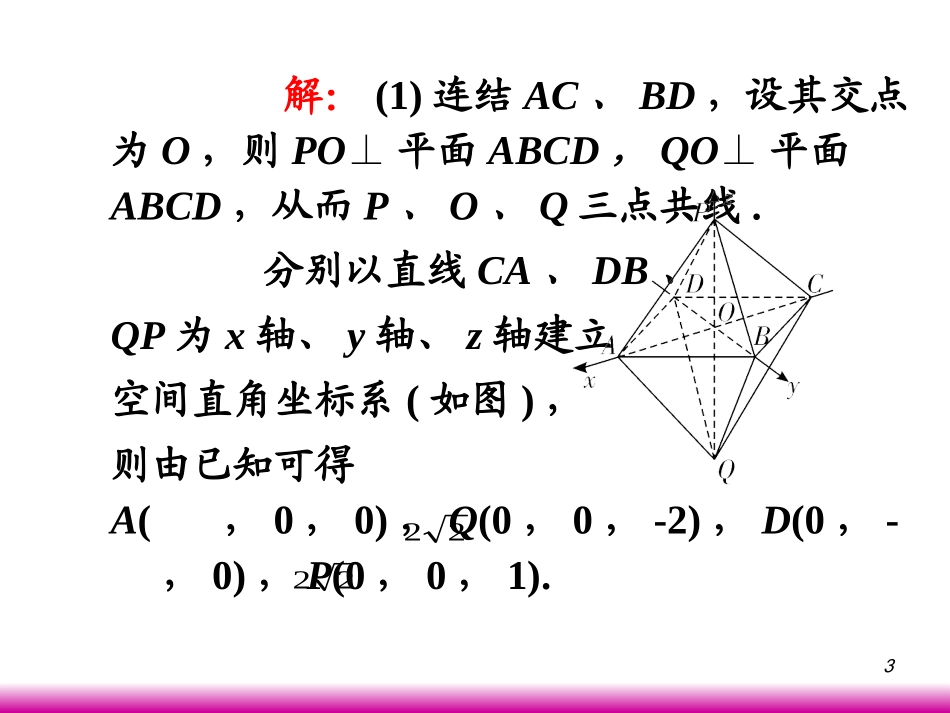
1第九章直线、平面、简单的几何体21.如图，已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2，AB=4.(1)求直线PQ与平面ADQ所成的角;(2)求异面直线AQ与PB所成的角.题型4空间角的计算第二课时3解：(1)连结AC、BD，设其交点为O，则PO⊥平面ABCD，QO⊥平面ABCD，从而P、O、Q三点共线.分别以直线CA、DB、QP为x轴、y轴、z轴建立空间直角坐标系(如图)，则由已知可得A(，0，0)，Q(0，0，-2)，D(0，-，0)，P(0，0，1).22224所以=(0，0，-3)，=(-，0，-2)，=(0，，-2).设n=(x，y，z)是平面ADQ的一个法向量.由，得取x=1，则z=-，y=-1，所以n=(1，-1，-).PQAQ22DQ2200DQnAQn02220222zyzx225设直线PQ与平面ADQ所成的角为θ，则sinθ=|cos〈n，〉|所以θ=.故直线PQ与平面ADQ所成的角为.(2)因为B(0，，0)，所以=(0，，-1).又=(-，0，-2)，所以cos〈，〉=.故异面直线AQ与PB所成的角为arccos.PQ22|PQnPQn|4Π4Π2222PBAQ22AQPB93PBAQPBAQ936点评：两向量的夹角公式可直接用来求两直线的夹角；而线面角可转化为直线对应的向量与平面的法向量所成的角；二面角可转化为两个平面的法向量所成的角.另外还需注意所求角与两向量夹角之间的关系.7如图，在长方体ABCD-A1B1C1D1中，已知AB=4，AD=3，AA1=2.E、F分别是线段AB、BC上的点，且EB=FB=1.(1)求二面角C-DE-C1的正切值；(2)求直线EC1与FD1所成角的余弦值.解：(1)以A为原点，AB,AD,AA1分别为x轴，y轴，z轴的正向，建立空间直角坐标系A-xyz.拓展练习拓展练习8则有D(0，3，0)、D1(0，3，2)、E(3，0，0)、F(4，1，0)、C1(4，3，2).于是=(3,-3,0),=(1,3,2),=(-4,2,2).设向量n=(x,y,z)与平面C1DE垂直，则有取z=2,则n=(-1,-1,2).则n是一个与平面C1DE垂直的向量.DE1EC1FD1ECnDEn21023033yxzyxyx9因为向量=(0，0，2)与平面CDE垂直观察图形知，n与所成的角θ即为二面角C-DE-C1的平面角.因为cosθ=所以tanθ=.所以二面角C-DE-C1的正切值为.(2)设EC1与FD1所成的角为β，则1AA1AA3640041122010111AAnAAn2222112222221114322221cos14132422EC·FD(-)βECFD()��102.长方体ABCD-A1B1C1D1中，AB=4，AD=6，AA1=4，M是A1C1的中点，P在线段BC上，且CP=2，Q是DD1的中点，求：(1)点M到直线PQ的距离;(2)点M到平面AB1P的距离.解：(1)如图所示，建立空间直角坐标系B-xyz，则A(4，0，0)，M(2，3，4)，P(0，4，0)，Q(4，6，2).题型5空间距离的计算11因为=(-2，-3，2)，=(-4，-2，-2)，所以在上的射影长为故点M到PQ的距离为QMOPQMOP6652410224222342222)()()()(-)(-)(-)(-)(-QPQP·QM.-)-(|MQ|d6462625176652212(2)设n=(x，y，z)是平面AB1P的法向量，则n⊥，n.⊥因为=(-4，0，4)，=(-4，4，0)，所以.因此可取n=(1，1，1).由于=(2，-3，-4)，那么点M到平面AB1P的距离为1AB点评：利用求向量的长度可求两点间的距离，而点到直线的距离或点到平面的距离可转化为向量的投影长度问题..|)(-)(-|nn|MA|d3353141312AP1ABAP044044yx-zx-1AB13在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点.(1)在侧面PAB内找一点N，使NE⊥平面PAC，并求出点N到AB和AP的距离；(2)求(1)中的点N到平面PAC的距离.3拓展练习拓展练习14解：(1)建立空间直角坐标系，如图.则A、B、C、D、P、E的坐标分别是A(0,0,0)、B(,0,0)、C(,1,0)、D(0,1,0)、P(0,0,2)、E(0,,1).依题意设N(x,0,z)，则=(-x,,1-z).由于⊥平面PAC，所以3321NE21NE,AC·NEAP·NE0015则，即解得，即点N的坐标为(,0,1)，从而点N到AB、AP的距离分别为1，.(2)设点N到平面PAC的距离为d，则0013(1210200(121),,-z),(-x,),,-z),(-x,,x-z-021301163zx6363331010136623121231062|(,,)(-,,)||ANNE|dNE(,,)��161.运用空间向量的坐标运算解决立体几何问题时，一般步骤为：(1)建立恰当的空间直角坐标系(例如:底面是矩形的直...