高考数学第一轮总复习9.7直线和平面所成的角与二面角(第2课时)课件 文 (广西专版) 课件VIP免费

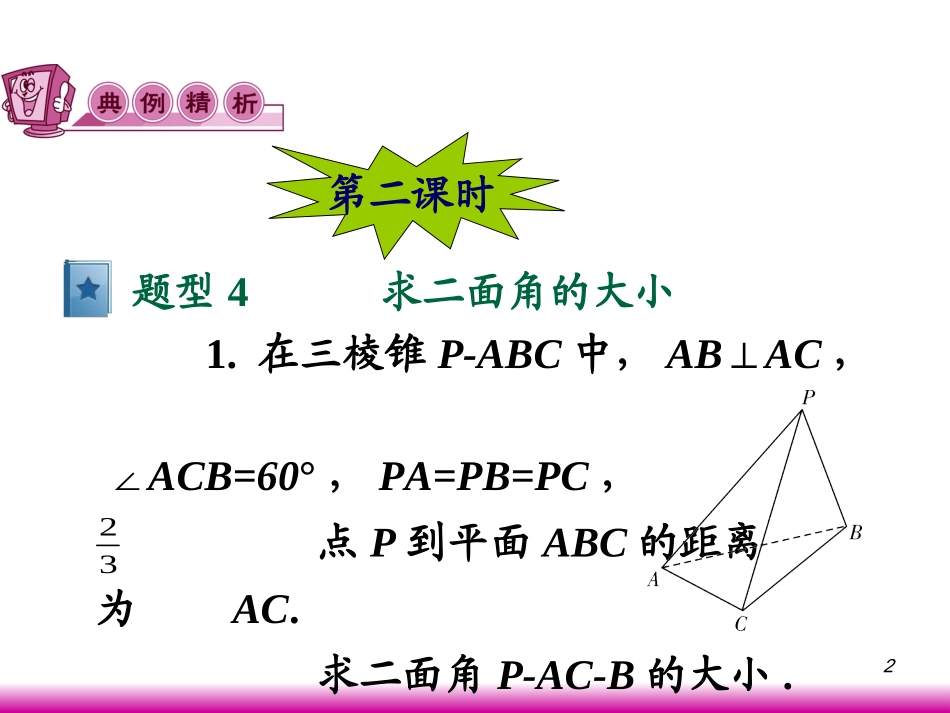
1第九章直线、平面、简单几何体21.在三棱锥P-ABC中，ABAC⊥，∠ACB=60°，PA=PB=PC，点P到平面ABC的距离为AC.求二面角P-AC-B的大小.题型4求二面角的大小第二课时323解法1：由条件知△ABC为直角三角形，且∠BAC=90°.因为PA=PB=PC，所以点P在平面ABC上的射影是△ABC的外心，即斜边BC的中点E.取AC的中点D，连结PD，DE，PE.因为PE⊥平面ABC，DE⊥AC(因为DEAB∥)，所以AC⊥PD.所以∠PDE就是二面角P-AC-B的平面角.4又PE=AC，DE=AC(因为∠ACB=60°)，所以，所以∠PDE=60°.故二面角P-AC-B的大小为60°.解法2：由条件知△ABC为直角三角形，且∠BAC=90°.因为PA=PB=PC，所以点P在平面ABC上的射影是△ABC的外心，即斜边BC的中点.2332323tanDEPEPDE235设O为BC的中点，取AC的中点D，连结PD，DO，PO，则PO⊥平面ABC.建立如图所示直角坐标系设AC=a，则A(a，-a，0)，B(-a，0，0)，C(a，0，0)，D(a，-a，0)，P(0，0，a).所以=(-a，a，0)，=(-a，a，a).因为AB⊥AC，又PA=PC，所以PD⊥AC，212332434323AB23DP4343236所以cos〈，〉即为二面角P-AC-B的余弦值.而cos〈，〉=所以二面角P-AC-B的大小为60°.AB2149163169043492304323432322222aaaaaaaaa)(a)(DPABDP7点评：求二面角的大小有两种方法：几何法与向量法.本题解法1是利用几何法来解决的，即按“一找、二证、三计算”三个步骤进行；解法2是利用向量法来解决的，即通过求垂直于两平面交线的直线的方向向量所成的角(需要注意是相等还是互补).8如图，直三棱柱ABC-A1B1C1中，ABAC,D⊥、E分别为AA1、B1C的中点，DE⊥平面BCC1.(1)证明：AB=AC;(2)设二面角A-BD-C为60°，求B1C与平面BCD所成的角的大小.解：(1)证法1：连结BE，因为ABC-A1B1C1为直三棱柱，所以∠B1BC=90°,拓展练习拓展练习9因为E为B1C的中点，所以BE=EC.又DE⊥平面BCC1，所以BD=DC(射影相等的两条斜线段相等).而DA⊥平面ABC，所以AB=AC(斜线段相等的射影相等)证法2：取BC的中点F，证四边形AFED为平行四边形，进而证AFDE∥，所以AF⊥BC，得AB=AC.10(2)作AGBD⊥于G，连结GC，则GCBD⊥，所以∠AGC为二面角A-BD-C的平面角，所以∠AGC=60°.不妨设AC=，则AG=2,GC=4.在RtABD△中，由AD·AB=易得AD=.32AGBD611设点B1到平面BCD的距离为h，B1C与平面BCD所成的角为α.由SB△1BC·DE=SBCD·h△，得解得h=，又B1C=,所以sinα=,所以α=30°.即B1C与平面BCD所成的角为30°.3131h632316626221313234211CBh122.在RtABC△中，∠ACB=30°，∠ABC=90°，D为AC的中点，E为BD的中点，连结AE并延长交BC于点F，将△ABC沿BD折成一个大小为θ的二面角A-BD-C.(1)证明：平面AEF⊥平面BCD(2)当θ为何值时，有AB⊥CD?题型4二面角背景下的位置关系分析13解：(1)证明：因为△ABC为直角三角形，∠ACB=30°，所以AB=AC.又D为AC的中点，所以AD=AC，所以AB=AD.因为E为BD的中点，所以AE⊥BD，所以BD⊥AE，BD⊥EF，所以BD⊥平面AEF.又BD平面BCD，所以平面AEF⊥平面BCD.212114(2)作AO⊥EF，垂足为O.因为平面AEF⊥平面BCD，所以AO⊥平面BCD.连结OB，则OB是AB在平面BCD内的射影所以AB⊥CDBO⊥CD.延长BO、CD相交于H，设AB=2a，则AE=ABcos30°=a.由△BEOBHD∽△，得.3BHBEDHOE15所以在RtAOE△中，cosAEO=∠.因为BD⊥平面AEF，所以θ=AEF=π-AEO=π-arccos.∠∠a.BDBDBDBHDHBEOE3323212131AEOE3116点评：与二面角有关的综合问题涉及到空间位置关系与空间角大小关系之间的综合.解决此类问题需注意几个转化：一是三维空间向二维空间的转化；二是空间角向线线角的转化；三是线面关系向线线关系的转化等.17拓展练习拓展练习在棱长为a的正方体OABC-O′A′B′C′中，E、F分别是棱AB、BC上的动点，且AE=BF.(1)求证：A′F⊥C′E；(2)当三棱锥B′-BEF的体积取得最大值时，求二面角B′-EF-B的大小(结果用反三角函数表示).18解：(1)证明：如图，以O为原点建立空间直角坐标系.设AE=BF=x，则A′(a，0，a)，F(a-x，a，0)，C′(0，a，a)，E(a，x，0)，所以=(-x，a，-a)，=(a，x-a，-a).因为=-xa+a(x-a)+a2=0，所以A′F⊥C′E.EC·FAFAEC19(2)记BE=y，则x+y=a.故三...