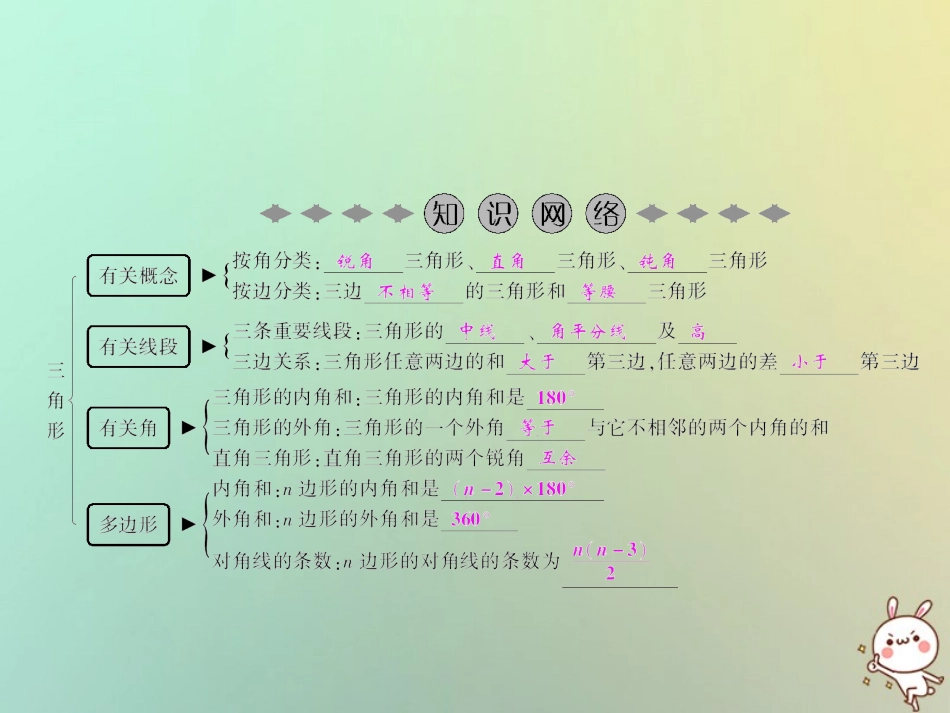
第十一章三角形章末小结2018秋季数学八年级上册•R【易错警示】1.判断三条线段能否组成三角形时,误认为只要有两条线段的长度之和大于第三条线段的长度就可以.2.根据等腰三角形腰上的中线分三角形为两部分,求底、腰时,容易漏解.3.运用三角形内角和定理的推论时,忽略条件“不相邻”而出错.4.一个多边形是正多边形必须具备“各个角都相等”“各条边都相等”这两个条件,缺一不可.5.画钝角三角形的高时,不知过哪一点画哪条边的垂线.6.在求三角形的边或周长时,容易忽略构成三角形的条件.【考点分类训练】与三角形有关的线段1.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是()A.5mB.15mC.20mD.28mD2.一个等腰三角形的两边长分别为4、8,则它的周长为()A.12B.16C.20D.16或203.生活中有一种可推拉的活动护栏,它是应用了数学中四边形的.4.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是.C不稳定性65.已知一个三角形的两边长分别为3和8,第三条边长为奇数,求第三条边的长.解:设第三条边的长为x,由题意,得8-3<x<8+3,所以5<x<11,又因为x为奇数,所以第三条边的长为7或9.6.如图所示:已知△ABC.(1)作出△ABC的三条高线;(2)如果△ABC的三边分别为AB=6,BC=5,AC=4,那么(1)中的三条高线的比是多少?解(1)如图所示:;(2)设AB、BC、AC边上的高为h1、h2、h3,根据题意,得6h1=5h2=4h3,所以h1∶h2∶h3=16∶15∶14=10∶12∶15.与三角形有关的角7.(长沙中考)一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形8.如图所示,图中∠α、∠β的度数分别是()A.30°,50°B.40°,80°C.40°,40°D.60°,40°BC9.(泰州中考)将一副三角板如图叠放,则图中∠α的度数为.10.已知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC=.15°99°或29°11.如图所示,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.解:∵AB∥CD,∠ABE=60°,∴∠EFC=∠ABE=60°.又∵∠D=50°,∠D+∠E=∠EFC,∴∠E=∠CFE-∠D=60°-50°=10°.12.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC,∠BOA的度数.解:∵AD是高,∴∠ADC=90°,∵∠C=66°∴∠DAC=180°-90°-66°=24°.∵∠BAC=54°,∠C=66°,AE是角平分线,∴∠BAO=27°,∠ABC=60°.∵BF是∠ABC的角平分线,∴∠ABO=30°,∴∠BOA=180°-∠BAO-∠ABO=123°.多边形的内角和与外角和13.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形.则这个多边形是边形.九14.如图,在四边形ABCD中,∠A=140°,∠D=80°.(1)如图①,若∠B=∠C,试求出∠C的度数;(2)如图②,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.解:(1)在四边形ABCD中,∠A+∠B+∠C+∠D=360°,∵∠A=140°,∠D=80°,∠B=∠C,∴140°+80°+2∠C=360°,∴∠C=70°;(2)∵∠A=140°,∠D=80°,BE∥AD,∴∠ABE=180°-∠A=180°-140°=40°,∠BED=180°-∠D=180°-80°=100°.又∵BE是∠ABC的角平分线,∴∠EBC=∠ABE=40°.∴∠C=∠BED-∠EBC=100°-40°=60°;(3)∵∠A=140°,∠D=80°,∠ABC+∠BCD=360°-(∠A+∠D)=360°-(140°+80°)=140°,又∵BE、CE分别是∠ABC、∠BCD的角平分线,∴∠EBC+∠ECB=12∠ABC+12∠BCD=12(∠ABC+∠BCD)=12×140°=70°.∴在△BEC中,∠BEC=180°-(∠EBC+∠ECB)=180°-70°=110°.