校高一数学向量小结与复习课件一 人教版 课件VIP免费

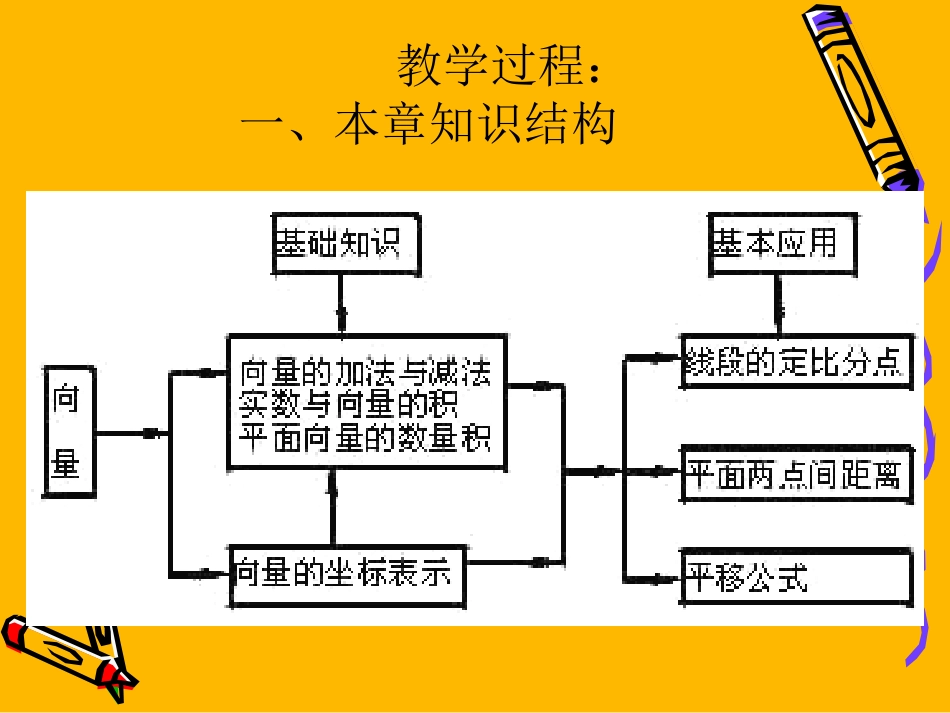
第五章向量小结与复习第五章向量小结与复习(1)(1)第五章向量小结与复习第五章向量小结与复习(1)(1)阆中东风中学校阆中东风中学校课题：向量小结与复习（1）教学目的：1、了解本章知识网络结构；2、进一步熟悉基本概念及运算律；3、理解重要定理、公式并能熟练应用；4、加强数学应用意识，提高分析问题，解决问题的能力5、认识事物之间的相互转化；6、培养学生的数学应用意识教学重点：突出本章重、难点内容教学难点：通过例题分析突出向量运算与实数运算的区别授课类型：复习课课时安排：1课时教具：多媒体、实物投影仪教学方法：自学辅导法在给出本章的知识网络结构后，列出复习提纲，引导学生补充相关内容，同时加强学生对基本概念、基本运算律、重要定理、公式的熟悉程度。教学过程：一、本章知识结构二、本章重点及难点(1)、本章的重点有向量的概念、运算及坐标表示，线段的定比分点，平移、正弦定理、余弦定理及其在解斜三角形中的应用；(2)、本章的难点是向量的概念，向量运算法则的理解和运用，已知两边和其中一边的角解斜三角形等；(3)、对于本章内容的学习，要注意体会数形结合的数学思想方法的应用。三、本章知识要点1、向量的概念•(1)、向量的基本要素：大小和方向；•(2)、向量的表示：几何表示法，坐标表示法;•(3)、向量的长度：即向量的大小，记作｜a｜；•(4)、特殊的向量：零向量a＝0|a|＝0,•单位向量为单位向量|a|＝1；•(5)、相等的向量：大小相等，方向相同;•(6)、平行向量(共线向量)：方向相同或相反的向量，称为平行向量记作”∥”，由于向量可以进行任意的平移(即自由向量)，平行向量总可以平移到同一直线上，故平行向量也称为共线向量。2、向量的运算(1)向量的运算和性质(表1)运算类型几何方法坐标方法运算性质向量的加法1平行四边形法则2三角形法则向量的减法三角形法则向量的数量乘法1、是一个向量,2、>0时,与a同向;<0时,与a异向;=0时,a=0∥),(2121yyxxbaabba)()(cbacbaACBCAB),(2121yyxxba)(babaBAABABOAOBa),(yxaaa)()(aaa)(baba)(baba3、向量的运算(2)•向量的运算和性质(表2)运算类型几何方法坐标方法运算性质向量的数量积是一个数1、或时=0,2且时,ba0a0bba0a0b||||cos,ababab2121yyxxbaabba()()()abababcbcacba)(22||aa22||yxa||||||baba4、重要定理和公式（1）•(1)平面向量基本定理e1,e2是同一平面内两个不共线的向量，那么，对于这个平面内任一向量a，有且仅有一对实数1,2使a=1e1+2e2•(2)两个向量平行的充要条件a∥ba＝λbx1y2-x2y1=0•(3)两个向量垂直的充要条件a⊥ba·b＝0x1y1+x2y2=04、重要定理和公式（2）(4)线段的定比分点公式设点P分有向线段所成的比为λ，即＝λ，点P的坐标为（x，y），则当λ＝1时，得中点公式：PP12PP.1,12121yyyxxx.2,22121yyyxxx4、重要定理和公式（3）(5)平移公式设点按向量平移后得到点，则=+或，曲线按向量移后所得的曲线的函数解析式为：(6)正、余弦定理正弦定理：余弦定理：),(kha),(yxPPOOPa.,kyyhxx)(xfy),(kha)(hxfky.2sinsinsinRCcBbAaAbccbacos2222Bacacbcos2222Cabbaccos2222四、讲解范例：例1、在四边形ABCD中·＝·＝·＝·，证明：四边形ABCD是矩形。分析：要证明四边形ABCD是矩形，可以先证四边形ABCD为平行四边形，再证明其一组邻边互相垂直为此我们将从四边形的边的长度和位置两方面的关系来进行思考证明：设＝a，＝b，＝c，＝d，则 a＋b＋c＋d＝O∴a＋b＝－（c＋d)两边平方得|a|2＋2a·b＋|b|2＝|c|2＋2c·d＋|d|2，又a·b＝c·d∴|a|2＋|b|2＝|c|2＋|d|2（1）BCABCDDACDDABCCDABDABCAB同理|a|2＋|d|2＝|b|2＋|c|...