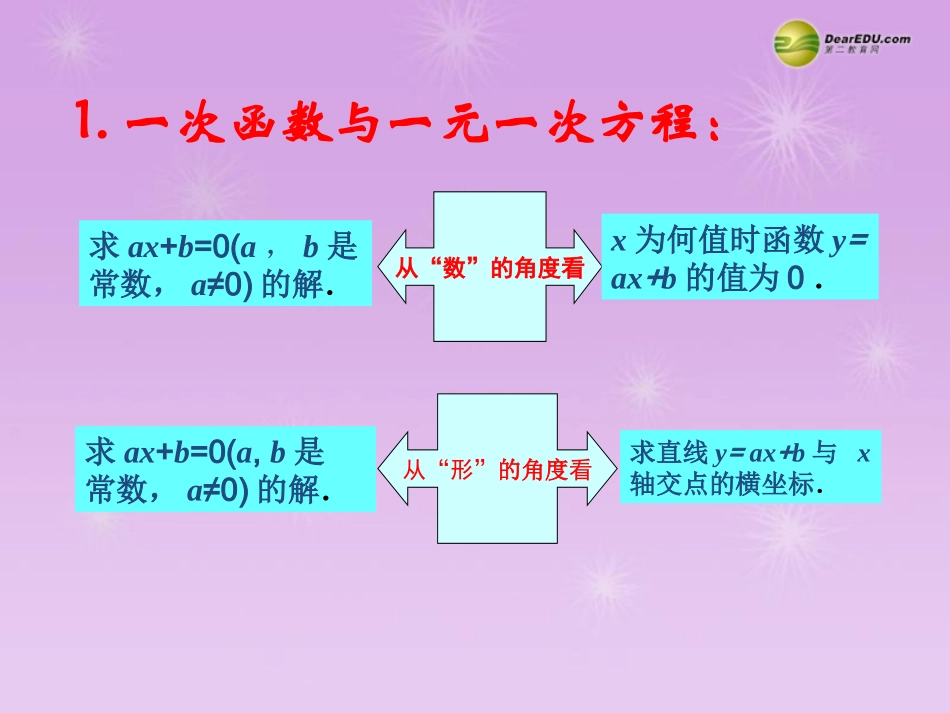
第十九章一次函数第第22课时课时章末小结章末小结如图,l1、l2分别表示张强步行与李华骑车在同一路上行驶的路程s与时间t的关系.(1)李华出发时与张强相距千米.(2)李华行驶了一段路后,自行车发生故障,进行修理,所用的时间是小时.(3)李华出发后小时与张强相遇.(4)若李华的自行车不发生故障,保持出发时的速度前进,小时与张强相遇,相遇点离李华的出发点千米.在图中表示出这个相遇点C.1013115C1.一次函数与一元一次方程:从“数”的角度看从“形”的角度看求ax+b=0(a,b是常数,a≠0)的解.求ax+b=0(a,b是常数,a≠0)的解.x为何值时函数y=ax+b的值为0.求直线y=ax+b与x轴交点的横坐标.2.一次函数与一元一次不等式:从“数”的角度看从“形”的角度看解不等式ax+b>0(a,b是常数,a≠0).x为何值时函数y=ax+b的值大于0.解不等式ax+b>0(a,b是常数,a≠0).求直线y=ax+b在x轴上方的部分(射线)所对应的的横坐标的取值范围.3.一次函数与二元一次方程组:解方程组自变量(x)为何值时两个函数的值相等.并求出这个函数值从“数”的角度看解方程组确定两直线交点的坐标.从“形”的角度看cbacbayxyx222111cbacbayxyx2221111.下列函数中,y随x的增大而减小的有()①②③④A.1个B.2个C.3个D.4个2.已知一次函数的图象如图所示,当时,y的取值范围是()A.B.C.D.3.已知mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标是________.12xyxy6133xyxy)21(02x20y40y2y4yO2-4xyCB(-2,0)4.直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是____.5.直线l1:与直线l2:在同一平面直角坐标系中,图象如图所示,则关于x的不等式的解集为,方程组的解为.bxky11xky22bxkxk124x<-223xy1122,kbykxy探究1重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:(1)分别写出当0≤x≤200、200<x≤400、400<x时,y与x的函数解析式;(2)利用函数解析式说明电力公司采用的收费标准;(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?200400104261.5450218xyO200400104261.5450218xy提问1:从图上你得到了哪些信息?这些信息对于解决问(1)有什么作用?重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:(1)分别写出当0≤x≤200、200<x≤400、400<x时,y与x的函数解析式;(2)利用函数解析式说明电力公司采用的收费标准;(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?探究1O200400104261.5450218xy重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:(1)分别写出当0≤x≤200、200<x≤400、400<x时,y与x的函数解析式;(2)利用函数解析式说明电力公司采用的收费标准;(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?提问2:如何根据解析式获得电力公司的收费标准?一次函数解析式中一次项系数的实际意义是什么?不用求解析式可以直接从图象上获得吗?探究1O200400104261.5450218xy重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:(1)分别写出当0≤x≤200、200<x≤400、400<x时,y与x的函数解析式;(2)利用函数解析式说明电力公司采用的收费标准;(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?提问3:电力公司的收费标准有几档?每档的自变量取值范围分别是什么?如何知道8月用电量的档位?探究1O解:(1)由图象可知,当0≤x≤200时,y是x的正比例...