江西省鹰潭市贵溪市第二中学九年级数学下册 28.1 锐角三角函数课件1 (新版)新人教版 课件VIP免费

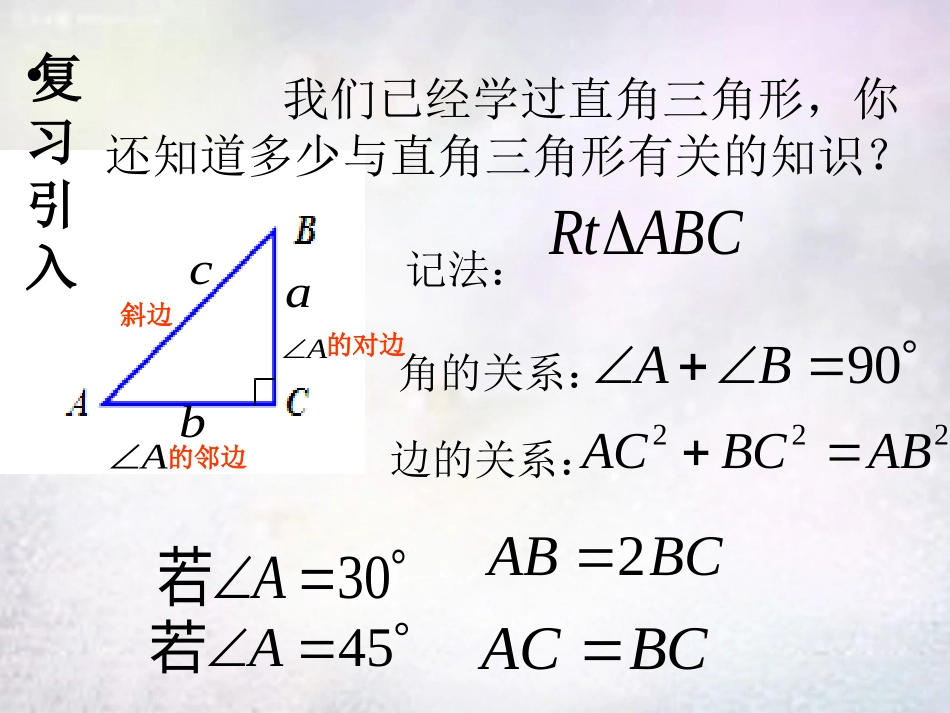
锐角三角函数—正弦•复习引入222ACBCABRtABC90AB我们已经学过直角三角形，你还知道多少与直角三角形有关的知识？记法：角的关系：边的关系：30A若2ABBC45A若ACBCbAa的对边c斜边A的邻边问题要从山脚A点向山上铺水管，测得山坡与水平面所成角的度数是30°，B点的高度为300米，D点的高度为500米，若铺到B需水管多长，铺到D呢？实践探索分析：这个问题转化为：∠A＝30°，BC、DE垂直AE,其中BC=300m，DE=500m,求AB、AD.根据：在直角三角形中，30°角的对边等于斜边的一半ABDAB=600m结论：在直角三角形中，不管三角形的大小如何，都有030角的对边斜边30o500mABC300mDE┌┌12AD=1000m结论：在直角三角形中，不管三角形的大小如何，都有探究如图，任意画一个Rt△ABC，使∠C＝90°，∠A＝45°，计算∠A的对边与斜边的比，你能得出什么结论？ABBCABC实践探索45°分析：在RtABC△中，∠C＝90°，由于∠A＝45°，所以RtABC△是等腰直角三角形。令BC=，那么AC=___,AB=_____.那么BCAB2aa1222aa2ao45角的对边斜边22综上可知：在一个RtABC△中，∠C＝90°实践探索ABC30°12A的对边斜边当∠A＝30°当∠A＝45°22A的对边斜边A的对边斜边当∠A＝α=固定值？这个该怎样证明呢？猜想任意画Rt△ABC和Rt△A’B’C’，使得∠C＝∠C’＝90°，其中∠A＝∠A’＝α，那么与相等吗？为什么？实践探索BCAB''''BCAB在图中，由于∠C＝∠C'＝90°，∠A＝∠A'＝α，所以Rt△ABCRt∽△A'B'C'''''BCABBCAB''''BACBABBC这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，都是一个固定值．A的对边斜边=固定值A的对边斜边如图，在Rt△ABC中，∠C＝90°，我们有认识正弦A的对边斜边122230°45°度数一定固定值∠A叫做∠A的正弦（英文名sine），记作sinA.即sinAA的对边斜边acsin30sin45┌∠A的对边ABCcab斜边sinA注意：1、sinA不是sin与A的乘积，而是一个整体；2、正弦的三种表示方式：sinA、sin56°、sinBAC∠3、sinA是线段之间的一个比值,没有单位。1222快速抢答sinAsinA5813sinAsinB3332快速抢答教学互动例1如图，在Rt△ABC中，∠C＝90°，求sinA和sinB的值．解：（1）在Rt△ABC中3sin5BCAAB54sinABACB（2）在Rt△ABC中135sinABBCA222213512ACABBC12sin13ACBAB2222435ABACBC练习如图，求sinA和sinB.教学互动解：在Rt△ABC中22225334ABACBC3334sin3434BCAAB5534sin3434ACBAB课后小结caAA斜边的对边sin1sin3022sin452如图，在Rt△ABC中，∠C＝90°┌∠A的对边ABCcab斜边作业：PT