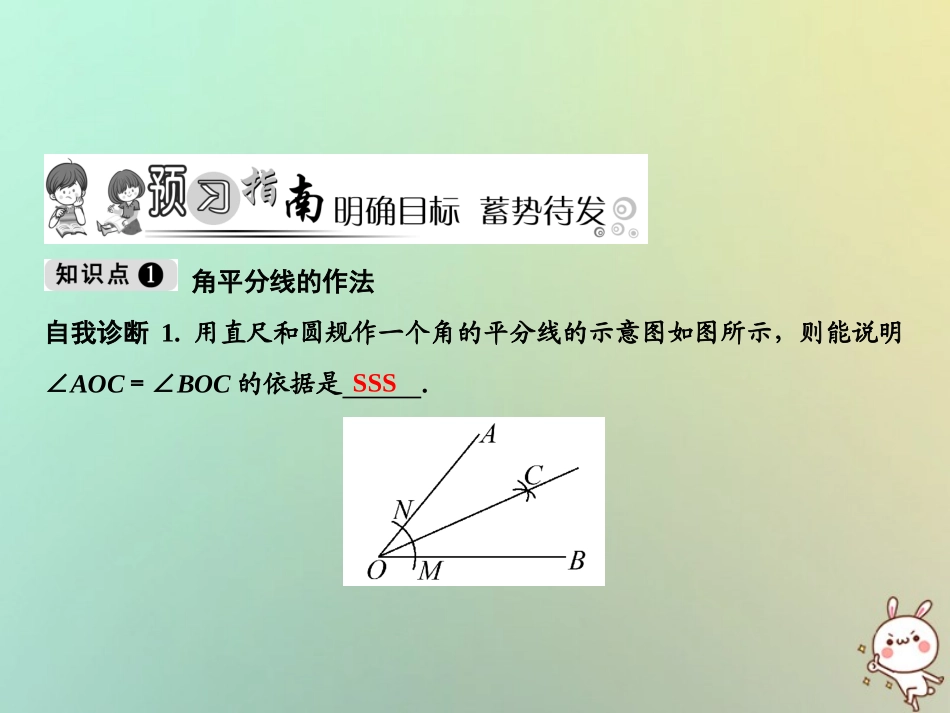
第十二章全等三角形12.3角的平分线的性质2018秋季数学八年级上册•R角平分线的作法自我诊断1.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是.SSS角平分线的性质角的平分线上的点到角的两边的距离.自我诊断2.已知OC是∠AOB的角平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长为.相等10角平分线的判定角的内部到角的两边的距离相等的点在上.自我诊断3.已知点P为∠AOB内部的一点,PD⊥OB于点D,PC⊥OA于点C,且PC=PD,则OP平分.易错点:忽略“到角的两边的距离”而致错.角的平分线∠AOB自我诊断4.如图所示,下列推理:①因为OC平分∠AOB,点P、D、E分别在OC、OA、OB上,所以PD=PE;②因为点P在OC上,PD⊥OA,PE⊥OB,所以PD=PE;③因为点P在OC上,PD⊥OA,PE⊥OB,且OC平分∠AOB,所以PD=PE.其中正确的个数是()A.0B.1C.2D.3B1.(怀化中考)如图所示,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别为C、D,则下列结论错误的是()A.PC=PDB.∠CPO=∠DOPC.∠CPO=∠DPOD.OC=ODB2.如图,PC⊥OA于点C,PD⊥OB于点D,若PC=PD,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.不能确定B3.如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,且BC=9cm,BD=5cm,则DE=cm.44.如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:DE=DF.证明:连接AD.在△ABD和△ACD中,AB=ACBD=CDAD=AD,∴△ABD≌△ACD,∴∠BAD=∠CAD,即AD平分∠EAF,又∵DE⊥AB于E,DF⊥AC于F,∴DE=DF.5.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下列结论错误的是()A.BD+ED=BCB.DE平分∠ADBC.AD平分∠EDCD.ED+AC>ADB6.如图,OP平分∠AOB,PE⊥OA于E,点F是射线OB上一个动点,若PE=2,则PF的最小值为()A.1B.2C.3D.4B7.如图,已知PA⊥ON于A,PB⊥OM于B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=.8.(湘潭中考)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为E点,请任意写出一组相等的线段.55°BC=BE或DC=DE9.如图,铁路OA和铁路OB交于O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA、OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.解:作∠AOB的角平分线交AB于M,点M即为所求.10.如图,已知BE=CF,BF⊥AC于F,CE⊥AB于E,BF与CE交于点D.求证:AD平分∠BAC.证明:∵BF⊥AC,CE⊥AB,∴∠DEB=∠DFC=90°,在△DEB和△DFC中,∠BDE=∠CDF对顶角相等∠DEB=∠DFCBE=CF,∴△DEB≌△DFC(AAS),∴DE=DF,∴点D在∠BAC的平分线上,∴AD平分∠BAC.11.如图所示,已知AD∥BC,DC⊥AD,∠BAD的平分线交CD于点E,且点E是CD的中点.问:(1)点E在∠ABC的角平分线上吗?(2)AD+BC与AB的大小关系怎样?请证明.解:(1)连接BE,作EH⊥AB于H,∵AE平分∠BAD,ED⊥AD,EH⊥AB,∴ED=EH.∵点E是CD的中点,∴ED=EC,∴EC=EH.而AD∥BC,DC⊥AD,∴EC⊥BC,∴BE平分∠ABC,即点E在∠ABC的平分线上;(2)AD+BC=AB.∵在Rt△ADE和Rt△AHE中,AE=AEED=EH,∴Rt△ADE≌Rt△AHE,∴AD=AH.同样可证明Rt△BCE≌Rt△BHE,∴BC=BH,∴AD+BC=AH+BH=AB.