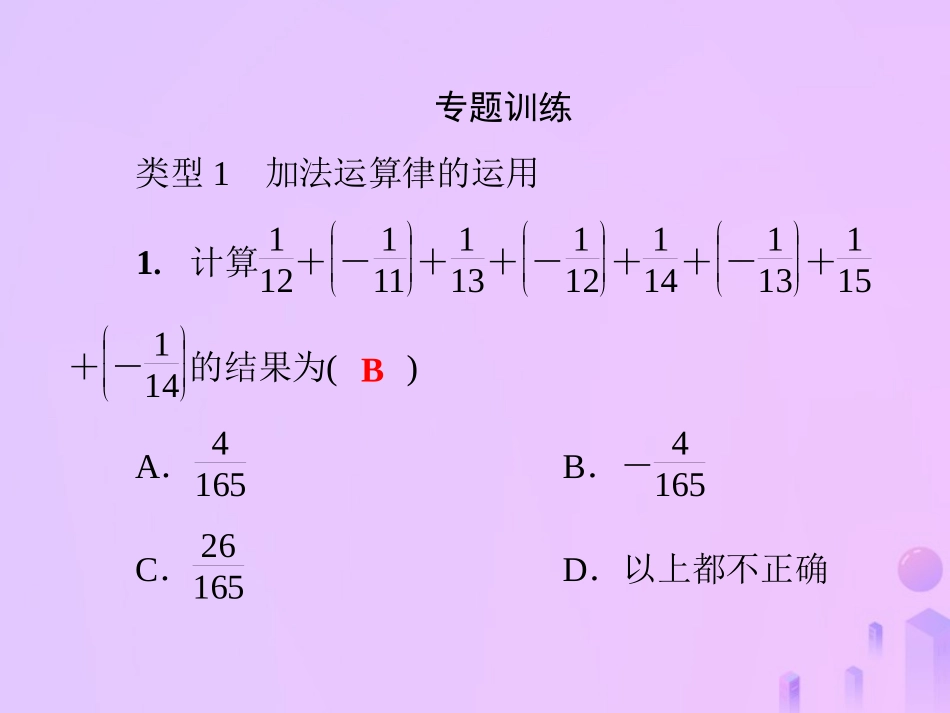
第2章有理数微专题1有理数的运算技巧专题解读有理数的运算首先是确定符号,然后再确定绝对值,具体到每个题,就要根据实际问题具体分析,运用交换律、结合律、分配律及逆向运用分配律,把具有某些特征的数或式子分别结合在一起进行计算,可以达到简化运算过程、减小运算量的目的.有理数混合运算的技巧很多,如:(1)正、负数分别相加;(2)同分母或小数部分相同的数相加;(3)互为相反数的两数相加;(4)除法转化为乘法;(5)正向或逆向运用分配律等.专题训练类型1加法运算律的运用1.计算112+-111+113+-112+114+-113+115+-114的结果为()A.4165B.-4165C.26165D.以上都不正确B2.计算下列各题.(1)23+(-16)-(-7)-17;解:原式=-3;(2)-3.72-1.23+4.18-2.93-1.25+3.72;解:原式=-1.23;(3)137+-213+247+-123.解:原式=0.(4)|13-12|+|14-13|+|15-14|+|16-15|.解:原式=12-13+13-14+14-15+15-16=12-16=13.3.两个小朋友玩跳棋游戏,游戏的规则是:先画一根数轴,棋子落在数轴上k0点,第一步从k0向左跳1个单位到k1,第二步从k1向右跳2个单位到k2,第三步从k2向左跳3个单位到k3,第四步从k3向右跳4个单位到k4,…,如此跳20步,棋子落在数轴的k20点,若k20表示的数是18,问k0的值为多少?解:由题意,得k0-1+2-3+4+…-19+20=18,即k0+10=18,所以k0=8.4.悟空随师父扫完金光塔回来,累得唐僧满头大汗,八戒见状,忙端茶向前献殷勤,并关切地说道:“师父,你这是扫了多少地啊,累成这个样子?”还未等唐僧说话,悟空抢言道:“傻猪头,你算算吧,塔共六层,以100平方米为标准,每层超过的平方米数记为正数,不足的平方米数记为负数,记录如下:+30,+18,+10,0,-15,-25.”八戒看后傻了眼,嘟嘟囔囔地说:“这咋算?”请你帮八戒算出来.解:(+30)+(+18)+(+10)+0+(-15)+(-25)=18(平方米).100×6+18=618(平方米).答:扫了618平方米.类型2乘法分配律的运用5.用简便方法计算(-23)×25-6×25+18×25+25,逆用分配律正确的是()A.25×(-23-6+18)B.25×(-23-6+18+1)C.-25×(23+6+18)D.-25×(23+6-18+1)B6.计算1357×316,最简便的方法是()A.13+57×316B.14-27×316C.10+357×316D.16-227×316D7.计算:(1)1112-56+78-2324×(-48);解:原式=-1112×48+56×48-78×48+2324×48=-44+40-42+46=0;(2)(-370)×-14+0.25×24.5+(-25%)×-512.解:原式=370×14+14×24.5+14×512=14×(370+24.5+5.5)=14×400=100;8.请你参考黑板中老师的讲解,用运算律简便计算:(1)999×(-15);解:999×(-15)=(1000-1)×(-15)=1000×(-15)+15=-15000+15=-14985;(2)999×11845+999×(-15)-999×1835.解:999×11845+999×(-15)-999×1835=999×(11845-15-1835)=999×100=99900.类型3错位相减法、裂项对消法的运用9.14×5+15×6+16×7+17×8.解:原式=14-15+15-16+16-17+17-18=14-18=18.10.(2017·菏泽模拟)阅读材料,求值:1+2+22+23+24+…+22015.解:设S=1+2+22+23+24+…+22015,将等式两边同时乘2得:2S=2+22+23+24+…+22015+22016,将下式减去上式得2S-S=22016-1,即S=1+2+22+23+24+…+22015=22016-1.请你仿照此法计算:(1)1+2+22+23+…+210;(2)1+3+32+33+34+…+3n(其中n为正整数).解:(1)设S=1+2+22+23+24+…+210,将等式两边同时乘2,得2S=2+22+23+24+…+211,将下式减去上式,得2S-S=211-1,即S=1+2+22+23+24+…+210=211-1;(2)设S=1+3+32+33+34+…+3n,将等式两边同时乘3,得3S=3+32+33+34+…+3n+1,将下式减去上式,得3S-S=3n+1-1,即2S=3n+1-1得S=1+3+32+33+34+…+3n=3n+1-12.类型4...