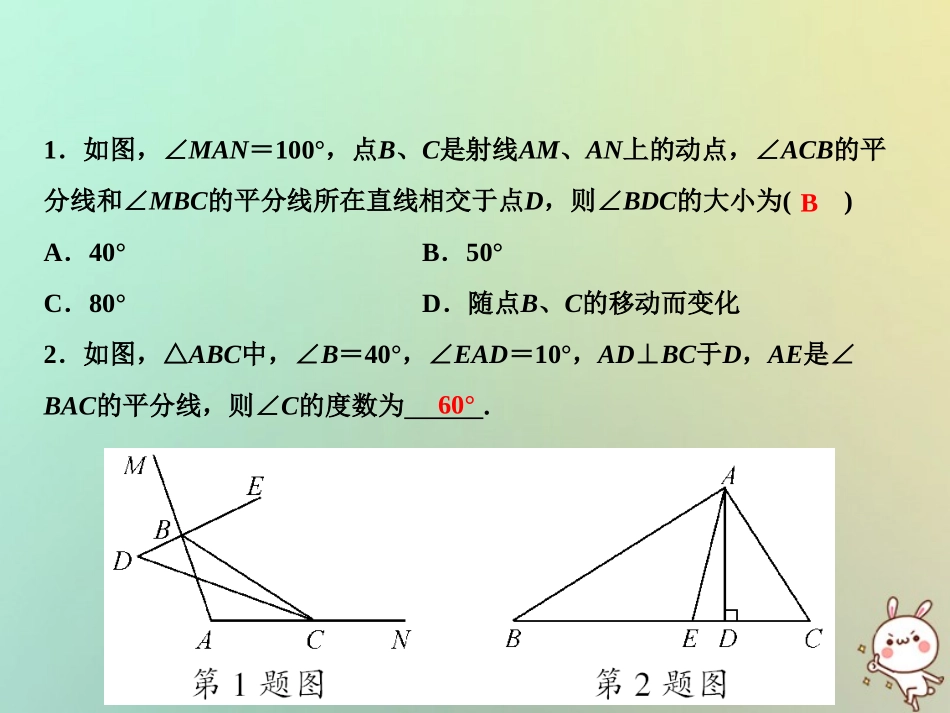
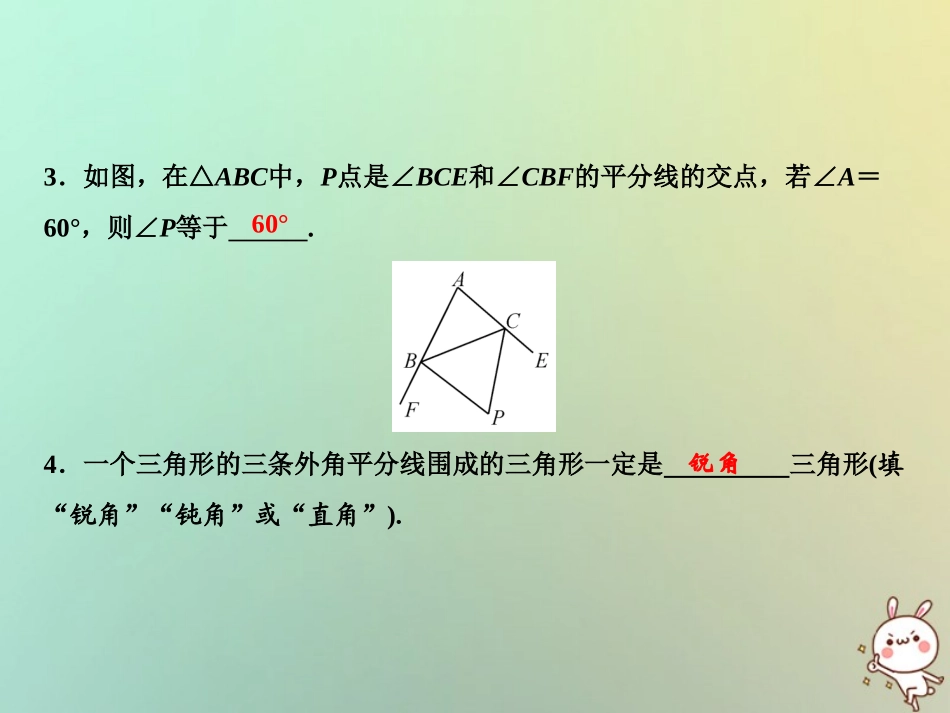
第13章三角形中的边角关系、命题与证明专题强化四三角形角平分线的应用2018秋季数学八年级上册•HK1.如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为()A.40°B.50°C.80°D.随点B、C的移动而变化2.如图,△ABC中,∠B=40°,∠EAD=10°,AD⊥BC于D,AE是∠BAC的平分线,则∠C的度数为.B60°3.如图,在△ABC中,P点是∠BCE和∠CBF的平分线的交点,若∠A=60°,则∠P等于.4.一个三角形的三条外角平分线围成的三角形一定是三角形(填“锐角”“钝角”或“直角”).60°锐角5.如图所示,在△ABC中,BO、CO是角平分线.(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由;解:∵BO、CO是角平分线,∴∠ABC=2∠OBC,∠ACB=2∠OCB.∵∠ABC+∠ACB+∠A=180°,∴2∠OBC+2∠OCB+∠A=180°,∵∠OBC+∠OCB+∠BOC=180°,∴2∠OBC+2∠OCB+2∠BOC=360°,∴2∠BOC-∠A=180°.∴∠BOC=90°+12∠A.∵∠ABC=50°,∠ACB=60°,∴∠A=180°-50°-60°=70°.∠BOC=90°+12×70°=125°;(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数;解:∠BOC=90°+12∠A=125°;(3)若∠A=n°,求∠BOC的度数.解:∠BOC=90°+12n°.6.如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.试判断∠F与∠B、∠D之间的等量关系.解:∠B+∠D=2∠F.理由:∵CF为∠BCD的平分线,EF为∠BED的平分线,∴∠DEF=∠BEF,∠DCF=∠BCF.∴∠D+2∠BEF+∠DAE=180°,∠B+2∠DCF+∠BAC=180°,又∵∠BAC=∠DAE,∴∠B+∠D+2∠BEF+2∠BAC+2∠DCF=360°,∵∠F+∠FNE+∠BEF=180°,∠FNE=∠DCF+∠BAC,∴∠F+∠BEF+∠DCF+∠BAC=180°.∴∠B+∠D=2∠F.