高一数学 三角函数模型的应用 课件VIP免费

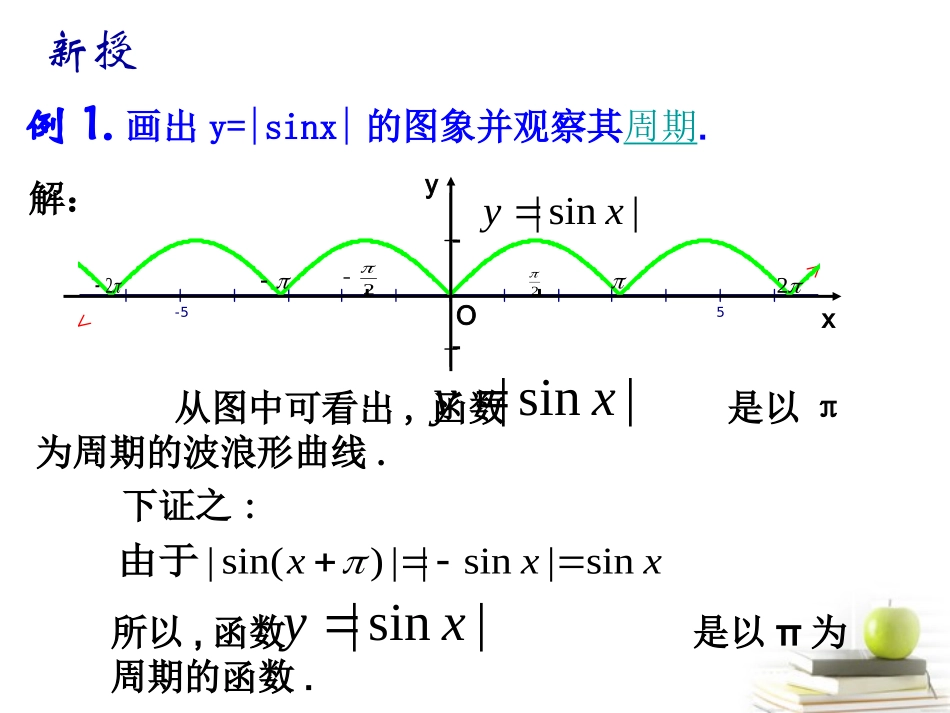
学习目标：1.会用三角函数解决一些简单的实际问题；2．体会三角函数是描述周期性变化现象的重要函数模型．三角函数模型的简单应用引入:三角函数能够模拟许多周期现象.因此,在解决实际问题和物理问题中有着广泛的应用.-55例1.画出y=|sinx|的图象并观察其周期.yxO从图中可看出,函数是以π为周期的波浪形曲线.下证之:所以,函数是以π为周期的函数.解：|sin|xy|sin|xy|sin|xyxxxsin|sin||)sin(|由于2222新授练习:(1)求函数y=|cosx|的周期.(2)求函数y=|tanx|的周期.（3)求函数y=|cosx+0.5|的周期.2)3()2()1(例2.如图,某地一天从6~14时的温度变化曲线近似满足函数(1)求这一天的最大温度差;(2)写出这段曲线的函数解析式..)sin(bxAy302010yxT/°Ct/h14610解:(1)由图可知,这段时间的最大温度差是20°C;(2)从图中可看出,从6~14时的图象是函数的半个周期的图象,故将x=6,y=10代入上式,解得综上,所求解析式为bxAy)sin(,2021030,1021030bA.8,61422143].14,6[,20)438sin(10xxy小结：maxmin1A=fx-fx2maxmin1b=fx+fx2利用求得2πT=，ωω一般的，所求出的函数模型只能近似刻画这天某个时刻的温度变化情况，因此应当特别注意自变量的变化范围.利用最高点或最低点在图像上，该点的坐标满足函数解析式求得；也可以利用函数的零值点来求．例3.海水受日月的引力，在一定的时候发生涨落的现象叫潮。一般地，早潮叫潮，晚潮叫汐。在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋。下面是某港口在某季节每天的时间与水深关系表：时刻时刻水深水深((米米))时刻时刻水深水深((米米))时刻时刻水深水深((米米))0.000.005.005.009.009.002.502.5018.0018.005.005.003.003.007.507.5012.0012.005.005.0021.0021.002.502.506.006.005.005.0015.0015.007.507.5024.0024.005.005.00（1）选用一个函数来近似描述这个港口的水深与时间的函数关系，给出整点时的水深的近似数值（精确0.001）.解:以时间为横坐标,水深为纵坐标,画出散点图(如图).根据图象,可考虑用函数，刻画水深与时间之间的对应关系.从数据和图象可以得出:hxAy)sin(时刻时刻0011223344556677889910101111水深水深((米米))5.0005.0006.2506.2507.1657.1657.5007.5007.1657.1656.2506.2505.0005.0003.7543.7542.8352.8352.5002.5002.8352.8353.7543.754时刻时刻121213131414151516161717181819192020212122222323水深水深((米米))5.0005.0006.2506.2507.1657.1657.5007.5007.1657.1656.2506.2505.0005.0003.7543.7542.8352.8352.5002.5002.8352.8353.7543.754故这个港口的水深与间的关系可用近似描述.由上述关系式可得港口在整点时水深的近似值:.6,122;0,12,5,5.2得由TThA56sin5.2xy24211815129637.502.505.000（2）一条货船的吃水深度（船底与水面的距离）为4米，安全条例规定至少要有1.5米的安全间隙（船底与海洋底的距离），该船何时能进入港口？在港口能呆多久？解:(2)货船需要的安全水深为4+1.5=5.5米,所以当y≥5.5就可以进港，令由计算器可得,如图,在区间[0,12]内,函数的图象与直线y=5.5有两个交点A、B，因此.2.06sin,5.556sin5.2xx得56sin5.2xy.2014.020135792.02.0sin1.2014.06,2014.06xx或.6152.5,3848.0BAxx解得.6152.176152.512,3848.123848.012DCxx8642105DCBA150由函数的周期性可得故货船可在凌晨零时30分左右进港，早晨5：30左右出港；或在中午12：30左右进港，下午17：30左右出港.每次可在港口停留5小时左右.（2）一条货船的吃水深度（船底与水面的距离）为4米，安全条例规定至少要有1.5米的安全间隙（船底与海洋底的距离），该船何时能进入港口？在港口能呆多久？（3）若某船的吃水深度为4米，安全间隙为1.5米，该船在2：00开始卸货，吃水深度以每小时0.3米的速度减少，那么该船在什么时间必须停止卸货，将船驶向较深的水域？练习：练习：如图，某大风车的半径为...