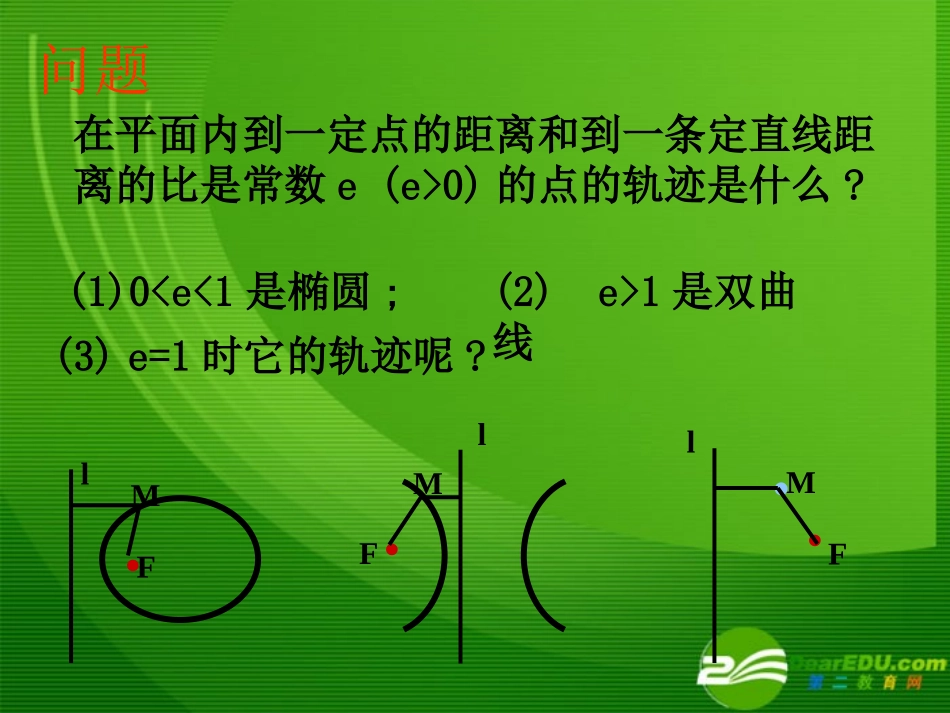
广西贵港市高中在平面内到一定点的距离和到一条定直线距离的比是常数e(e>0)的点的轨迹是什么?(1)01是双曲线l·FM·抛物线的生活实例抛物线的生活实例抛球运动平面内与一个定点F和一条定直线l的距离相等的点M的轨迹叫做抛物线抛物线定义定义··FMlN定点F---抛物线的焦点焦点定直线l---抛物线的准线准线即即::1,MFMMN则的轨迹方程为抛物线··FMlN标准方程求曲线方程的基本步骤是怎样的?(1)建系(2)设点(3)列式(4)化简(5)证明?yxoy=ax2+bx+cy=ax2+cy=ax2xyo··FMlNK设︱KF︱=p则F(,0),l:x=-p2p2设点M的坐标为(x,y),化简得y2=2px(p>0)取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴由定义可知,1MFMN22()22ppxyxp的几何意义:焦点:准线:顶点:开口方向:向右标准方程y2=2px(p>0)的特点:焦点到准线的距离F(p/2,0)在x轴的正半轴上x=-p/2原点(0,0)xyoFl图形标准方程焦点坐标准线方程y2=2px(p>0)y2=-2px(p>0)x2=-2py(p>0)x2=2py(p>0)xyo(,0)2p2px(,0)2pxyolFlxyoFxyolF(0,)2p(0,)2p2py2px2py如何判断抛物线的焦点位置,开口方向如何判断抛物线的焦点位置,开口方向??焦点位置看一次项开口方向看正负y2=(p>0)xyoFx2p例题((11)已知抛物线的标准方程是)已知抛物线的标准方程是求它的焦点坐标和准线方程;求它的焦点坐标和准线方程;26xy解:由题可知:2p=6,则p=333022y焦点为(,-),准线为xyolF(2)准线方程是x=14解:xyo11242pp由题可知,2yx反思抛物线的标准方程焦点坐标和准线方程:先定位,后定量1、求下列抛物线的焦点坐标和准线方程:21(1)2xy2(2)250yx课堂练习2(3),(0)xaya11(0,),88y焦点为准线方程为55(,0),88x焦点为准线方程为lxyoFxyolF210,ayxa若11(,0),,44xaa焦点为准线方程为210,||ayxa若11(,0),,4||4||xaa焦点为准线方程为11(,0),44xaa焦点为准线方程为xyoxyolF2、根据下列条件写出抛物线的标准方程:(1)焦点是F(3,0);(2)焦点到准线的距离是2;y2=12xy2=4x,y2=-4x,x2=4y,x2=-4y(3)过点A(-3,2)的抛物线的标准方程0yx.A22222,2,(0)92439423xpyypxpppxyyx设抛物线方程为或点A(-3,2)分别代入方程得,或,解:小结小结2、抛物线的定义,标准方程类型与图象的对应关系以及判断方法1、抛物线的定义、标准方程和它的焦点、准线、方程3、注重数形结合的思想。课后作业课本P119:2、3、4