函数的微分课件VIP免费

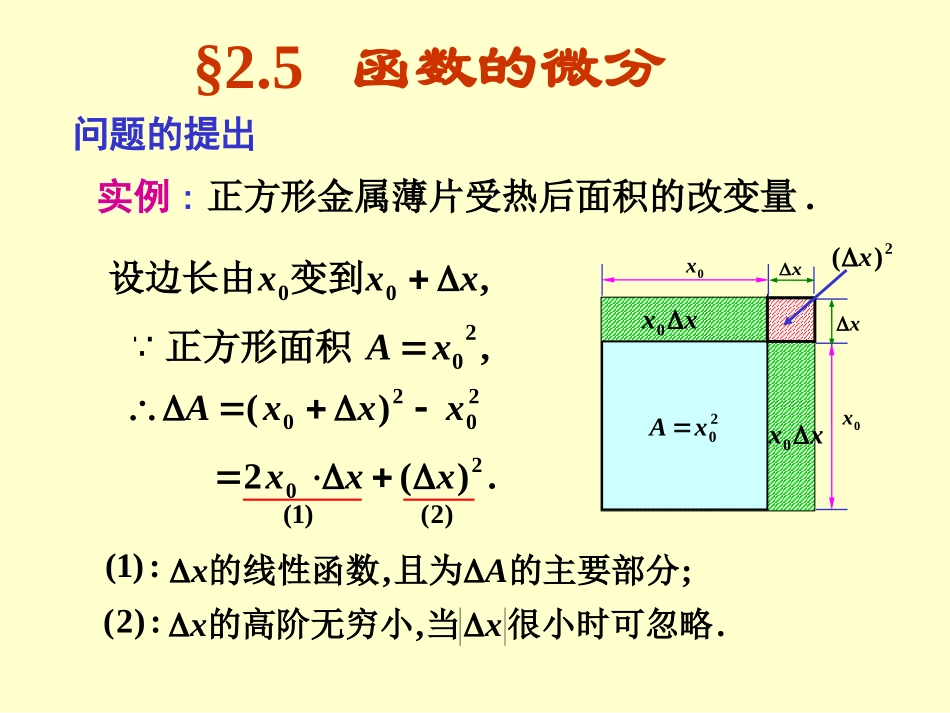
问题的提出实例:正方形金属薄片受热后面积的改变量.,00xxx变到设边长由0x0xxx,20xA正方形面积20xA2020)(xxxA.)(220xxx)1(xx0xx0:)1(;,的主要部分且为的线性函数Ax)2(2)(x:)2(.,很小时可忽略当的高阶无穷小xx§2.5函数的微分再例如,.,03yxxxy求函数的改变量时为处的改变量在点设函数3030)(xxxy.)()(3332020xxxxx)1()2(,很小时当x),()2(xox的高阶无穷小是.320xxy既容易计算又是较好的近似值问题:这个线性函数(改变量的主要部分)是否所有函数的改变量都有?它是什么?如何求?一、微分的定义定义:设函数y=f(x)在某区间I内有定义,x0及x0+x在区间I内,如果存在与x无关的常数A,使得y=f(x0+x)–f(x0)=A·x+o(x)成立,则称函数函数yy==ff((xx))在点在点xx00处可微处可微,并且称AA··xx为函数为函数yy==ff((xx))在点在点xx00处相应于自变量增量处相应于自变量增量xx的微分的微分,记作dy,即dy=A·x.微分dy叫作函数增量y的线性主部—微分的实质.由定义知:dyyxAxo)(1).0(1x(1)dy是自变量的改变量x的线性函数;(2)当时，y–dy=o(x)是x的高阶无穷小;(3)当A0时,当时，y与dy是等价无穷小;实际上(4)A是与x无关的常数,但与f(x0)和x0有关;(5)当|x|很小时,ydy=A·x(线性主部).二、可微的条件定理:函数f(x)在点x0处可微的充分必要条件是函数f(x)在点x0处可导,且dy=f(x0)·x.0x0x定理表明:可导可微,且f(x0)=A.在f(x0)0的条件下,当x→0时,y～dy,且yy––ddyy既是既是xx的高阶无穷小的高阶无穷小,,又是又是ddyy的高阶的高阶无穷小无穷小.因此dy也是y的主要部分.).(xfdxdy由于自变量对自己的导数等于1,所以通常把自变量的增量x称为自变量的微分,记作dx,即dx=x.所以,dy=f(x)dx.从而即函数的微分函数的微分ddyy与自变量的微分与自变量的微分ddxx之商就之商就等于该函数的导数等于该函数的导数,因此导数也叫做“微商微商”..)(),(,,)(xxfdyxdfdyxxfy即或记作微分称为函数的的微分在任意点函数三、微分的几何意义xyo)(xfy0xMT)xx0PNxydy)(xo则y是曲线C上关于点M的纵坐标的增量,当|x|很小时,在点M的附近用切线的增量近似代替曲线的增量.设曲线C的方程为y=f(x),曲线C上的点M处有切线.MM点处的切线对应点点处的切线对应点MM的纵的纵坐标的增量坐标的增量..而ddyy是曲线是曲线CC在在四、微分的求法dxxfdy)(求法:计算函数的导数,乘以自变量的微分.1.基本初等函数的微分公式xdxxxdxdxxxdxdxxdxdxxdxdxxdxdxxddxxxdCdcotcsc)(csctansec)(seccsc)(cotsec)(tansin)(coscos)(sin)(0)(221dxxxddxaxxddxeedadxaadaxxxx1)(lnln1)(log)(ln)(dxxxarcddxxxddxxxddxxxd222211)cot(11)(arctan11)(arccos11)(arcsin2.函数和、差、积、商的微分法则2)()()()(vudvvduvududvvduuvdCduCuddvduvud3.复合函数的微分法则),()(xfxfy有导数设函数;)(,)1(dxxfdyx是自变量时若则的可微函数即另一变量是中间变量时若),(,)2(txtx,)(dxdtt.)(dxxfdy.)()(dttxfdy结论:无论x是自变量还是中间变量,函数y=f(x)的微分形式总有:dxxfdy)(一阶微分形式的不变性例3:.)0,1(),sin(cosdyaaayx求设例4:.,sindybxeyax求设例5:dxdydybaeyxxy,,求设例6:.),1ln(2cosdyeyx求设例1:.),ln(2dyexyx求设例2:.,cos31dyxeyx求设1.函数的近似计算)(很小时x（3）计算附近的函数值0x))(()()(000xxxfxfxfxxfxfxxf)()()(000（2）计算增量的函数值xxfxfxxfy)()()(000即(4)在(3)式中取,且x接近0,于是得00xxffxf)0()0()(五、微分在近似计算中的应用（1）计算增量xxfdyy)(0应用(4)式可得以下公式(下面都假定是较小的数值)xxnxn111)1)(sin)2用弧度作单位来表达xxx)(tan)3用弧度作单位来表达xxxxx1e)4xx)1ln()...