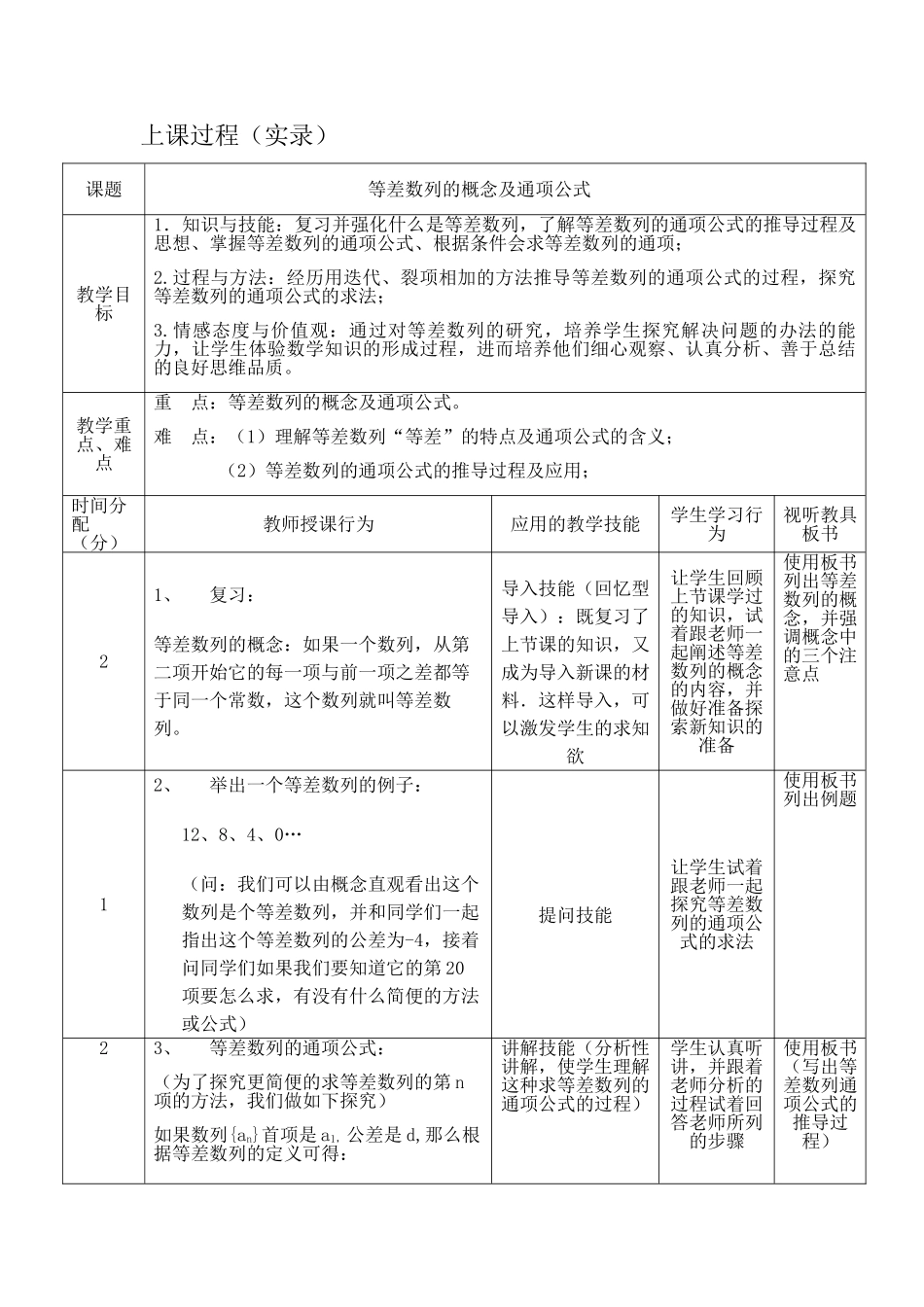
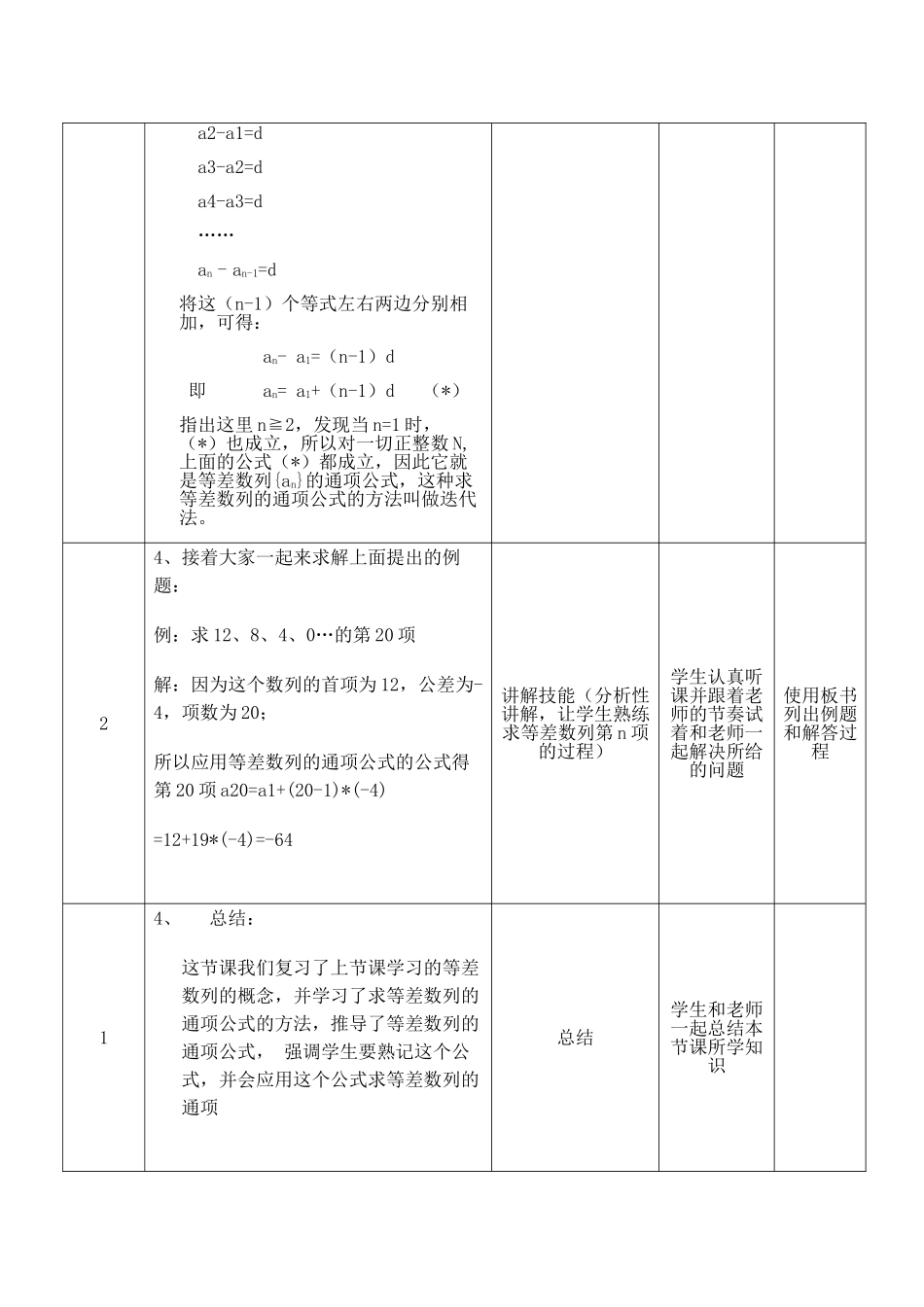
上课过程(实录)课题等差数列的概念及通项公式教学目标1.知识与技能:复习并强化什么是等差数列,了解等差数列的通项公式的推导过程及思想、掌握等差数列的通项公式、根据条件会求等差数列的通项;2.过程与方法:经历用迭代、裂项相加的方法推导等差数列的通项公式的过程,探究等差数列的通项公式的求法;3.情感态度与价值观:通过对等差数列的研究,培养学生探究解决问题的办法的能力,让学生体验数学知识的形成过程,进而培养他们细心观察、认真分析、善于总结的良好思维品质。教学重点、难点重 点:等差数列的概念及通项公式。难 点:(1)理解等差数列“等差”的特点及通项公式的含义; (2)等差数列的通项公式的推导过程及应用;时间分配(分)教师授课行为应用的教学技能学生学习行为视听教具板书21、复习:等差数列的概念:如果一个数列,从第二项开始它的每一项与前一项之差都等于同一个常数,这个数列就叫等差数列。导入技能(回忆型导入):既复习了上节课的知识,又成为导入新课的材料.这样导入,可以激发学生的求知欲让学生回顾上节课学过的知识,试着跟老师一起阐述等差数列的概念的内容,并做好准备探索新知识的准备使用板书列出等差数列的概念,并强调概念中的三个注意点12、举出一个等差数列的例子:12、8、4、0…(问:我们可以由概念直观看出这个数列是个等差数列,并和同学们一起指出这个等差数列的公差为-4,接着问同学们如果我们要知道它的第 20项要怎么求,有没有什么简便的方法或公式)提问技能让学生试着跟老师一起探究等差数列的通项公式的求法使用板书列出例题23、等差数列的通项公式:(为了探究更简便的求等差数列的第 n项的方法,我们做如下探究)如果数列{an}首项是 a1,公差是 d,那么根据等差数列的定义可得:讲解技能(分析性讲解,使学生理解这种求等差数列的通项公式的过程)学生认真听讲,并跟着老师分析的过程试着回答老师所列的步骤使用板书(写出等差数列通项公式的推导过程) a2-a1=d a3-a2=d a4-a3=d …… an - an-1=d将这(n-1)个等式左右两边分别相加,可得: an- a1=(n-1)d 即 an= a1+(n-1)d (*)指出这里 n≧2,发现当 n=1 时,(*)也成立,所以对一切正整数 N,上面的公式(*)都成立,因此它就是等差数列{an}的通项公式,这种求等差数列的通项公式的方法叫做迭代法。24、接着大家一起来求解上面提出的例题:例:求 12、8、4、0…的第 20 项解:因为这个数列的...