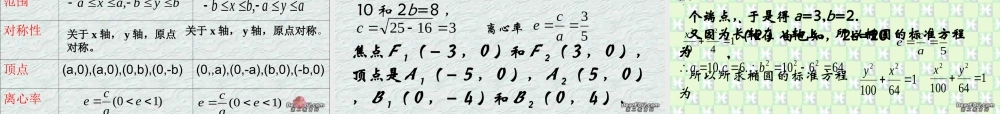高二数学椭圆圆锥曲线课件 新课标 课件VIP免费

椭圆的定义及标准方程 已知一曲线是与两个 定 点 O （ 0 ，0 ） 、 A （ 3 ，0 ）距离的比为的点的轨迹，求此曲线的方程，并画出曲线.到两定点距离之商等于常数的点的轨迹是圆，到两定点距离之和等于常数的点的轨迹是什么呢？结论：平面内与两个定点 F1 与 F2 距离的和等于常数 2a( 大于 ) 的点的轨迹为椭圆 平面内与两个定点 F1 与 F2 距离的和等于常数 2a( 等于 ) 的点的轨迹维修线段 平面内与两个定点 F1 与 F2 距离的和等于常数 2a( 小于 ) 的点不存在我们把平面内与两个定点 F1 、 F2 的距离的和等于常数（大于∣ F1F2∣ ）的点的轨迹叫椭圆 . 这两个定点叫椭圆的焦点，两焦点的距离叫椭圆的焦距 .下面我们来计算椭圆的方程，求曲线方程的一般步骤为什么？建立适当的坐标系 yx, 表示曲线上任意一点 M 的坐标 .写出适当条件 P 的 M 的集合 P={M|P(M)}用坐标表示条件 P(M) ，列出方程 f(x,y)=0化方程 f(x,y)=0 为最简形式证明以化简后的方程的解为坐标的都是曲线上的点如图建立直角坐标系 xoy ，设 M(x,y) 是椭圆上任意一点 0022121,,,,,ccFFCFF的坐标分别是那么由椭圆的定义aMFMFMP2|21aycxycx22222o1F02,cF0,cyxM,xy22222222caayaxca由椭圆的定义可知 2a>2c 即 a>c所以022 ca令0222bbca代入上式得222222bayaxb两边同时除以22ba得12222 byax如果焦点在 y 轴上，焦点坐标分别为F1(-c,0 ） ,F2(c,0) ， 那么方程为12222 bxay这个方程叫做椭圆的标准方程，它所表示的椭圆的焦点在 x 轴上，焦点是F1(-c,0 ） ,F2(c,0) ，这里 c2=a2-b2.例 1 求适合下列条件的椭圆的标准方程：（ 1 ）两个焦点的坐标分别是（－ 4 ， 0 ）（ 4 ， 0 ），椭圆上一点 P 到两焦点距离之和等于 10 （ 2 ）两个焦点的坐标分别是（ 0 ，－ 2 ）、（ 0 ， 2 ），并且椭圆经过点.解：（ 1 ）因为椭圆的焦点在 x 轴上，所以设它的标准方程为)0(12222babxay.由椭圆的定义知：102)225()23()225()23(2222∴a=10又 c=2 ∴b2=a2 － c2=6 所以所求椭圆方程为161022 xy2a=)25,23(例 2 已知 B 、 C 是两个定点，∣ BC =6∣，且△ABC 的周长等于 16 ，求顶点 A 的轨迹方程 .分析：在解析几何里，...