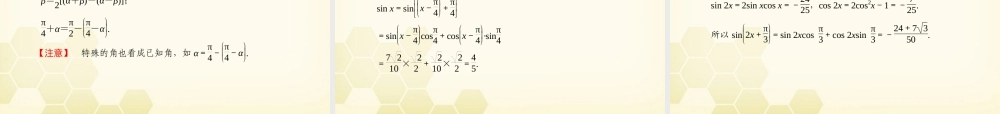高三数学一轮复习 第3章第5课时 两角和与差的正弦、余弦和正切公式精品课件 理 北师大版 课件VIP免费

• 第 5 课时 两角和与差的正弦、• 余弦和正切公式 •1 ．两角和与差的三角函数公式•sin(α±β) ＝ ；•cos(α±β) ＝ ；•tan(α±β) ＝.•其变形为：•tan α ＋ tan β ＝ ；•tan α － tan β ＝ ；•tan αtan β ＝.sin αcos β±cos αsin βcos_αcos_βsin_∓αsin_βtan α±tan β1∓tan αtan β. tan(α ＋ β)(1 － tan_αtan_β)tan(α － β)(1 ＋ tan_αtan_β)1－tan α＋tan βtanα＋β •2 ．二倍角公式•sin 2α ＝ ；•cos 2α ＝ ＝ ＝ ；•tan 2α ＝.【注意】 在公式 T(α±β)中，α、β、α±β 必须使等式两端均有意义，即 α、β、α±β 都不能取π2＋kπ(k∈Z)．否则，利用诱导公式求解． 2sin αcos αcos2α － sin2α2cos2α － 11 － 2sin2α2tan α1－tan2α •其公式变形为：•sin2α ＝ ；•cos2α ＝ .1－cos 2α2 1＋cos 2α2 1．计算 sin 43°cos 13°－cos 43°sin 13°的结果等于( ) A.12 B. 33 C. 22 D. 32 解析： sin 43°cos 13°－cos 43°sin 13°＝sin(43°－13°)＝sin 30°＝12.故选 A. 答案： A •答案： B 2．计算 1－2sin2 22.5°的结果等于( ) A.12 B. 22 C. 33 D. 32 解析： 1－2sin222.5°＝cos 45°＝ 22 . •答案： A 3．(2010·全国新课标卷)若 cos α＝－45，α 是第三象限的角，则sinα＋π4 ＝( ) A．－7 210 B.7 210 C．－ 210 D. 210 解析： 由于 α 是第三象限角且 cos α＝－45，∴sin α＝－35， ∴sinα＋π4 ＝sin αcosπ4＋cos αsin π4＝ 22 －45－35 ＝－ 710 2. 4．已知 tanα＋π4 ＝17，则 tan α＝________. 解析： 由 tanα＋π4 ＝17得1＋tan α1－tan α＝17， 所以 tan α＝－34. 答案： －34 5．若 sinπ2＋θ ＝35，则 cos 2θ＝________. 解析： 由 sinπ2＋θ ＝35，可得 cos θ＝35， ∴cos 2θ＝2cos2θ－1＝2×352－1＝－ 725. 答案： － 725 • 应熟悉公式的逆用和变形应用，公式的正用是常见的，但逆用和变形应用则往往容易被忽视，公式的逆用和变形应用更能开拓思路，培养从正向思维向逆向思维转化的能力，只有熟悉了公式的逆...