高二数学指数函数的图像和性质课件VIP免费

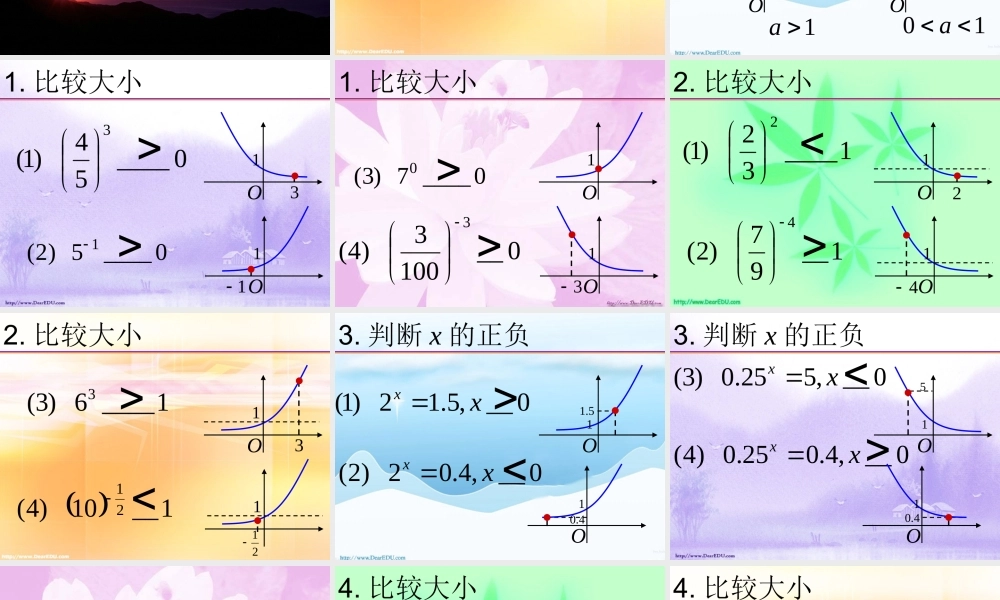
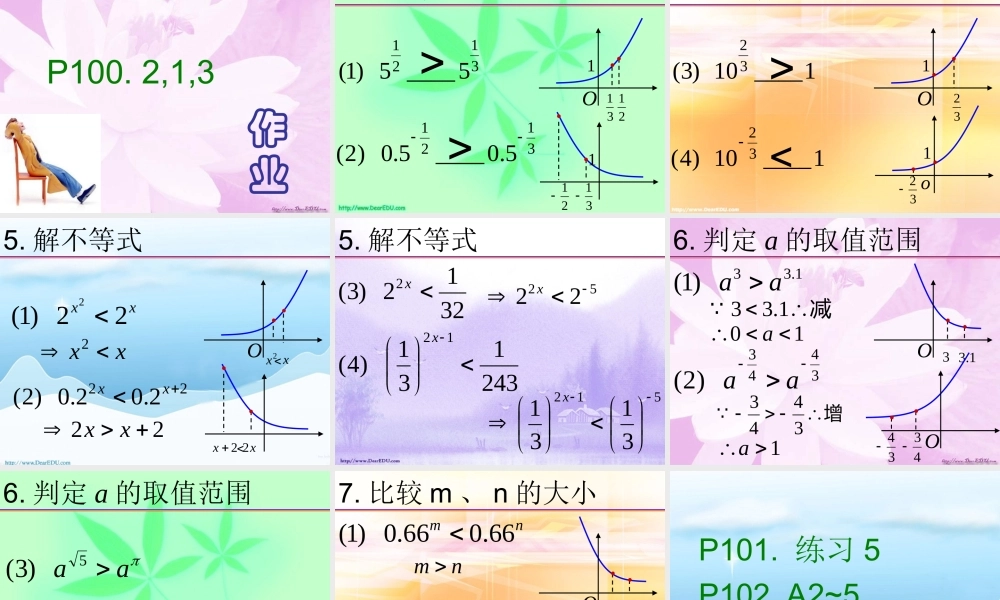
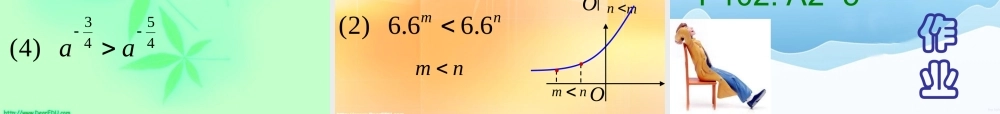四 . 指数函数与对数函数• 指数• 指数函数• 对数• 对数函数1. 根式?0.1n）且（1?.2nNnann??.3nnnnanan为偶数，为奇数，Nan 2. 有理指数幂的概念???0 a? na?nma? nma3. 运算法则? nm aa?nmaa?)(nma? nn ba指数函数1. 定义y=ax （ a>0 且 a≠1 ）， xR∈1. 图像和性质y=ax （ a>0 且 a≠1 ）O1O1O11a10 a1. 比较大小0____54)1(3O130____5)2(1O111. 比较大小0____7)3(0O10__1003)4(3O132. 比较大小1____32)1(2O11__97)2(4O1422. 比较大小1____6)3(3O1 1__10)4(2112133. 判断 x 的正负0__,5.12)1(xx O10__,4.02)2(xx 5.1O14.03. 判断 x 的正负0__,525.0)3(xx O10__,4.025.0)4(xx 5O14.0作P100. 2,1,3业4. 比较大小31215____5)1(O11312131215.0____5.0)2( 31214. 比较大小1____10)3(32O1321____10)4(32o1325. 解不等式xx22)1(2 O2xx222.02.0)2(xxx22xxx 222xx5. 解不等式3212)3(2 x243131)4(12x5222x5123131x6. 判定 a 的取值范围1.33)1(aa O 31.33443)2( aaO3443减1.33增34431a10a6. 判定 a 的取值范围aa5)3(4543)4( aa7. 比较 m 、 n 的大小nm66.066.0)1(O nmnm6.66.6)2(Omnnm nm 作P101. 练习 5P102. A2~5业