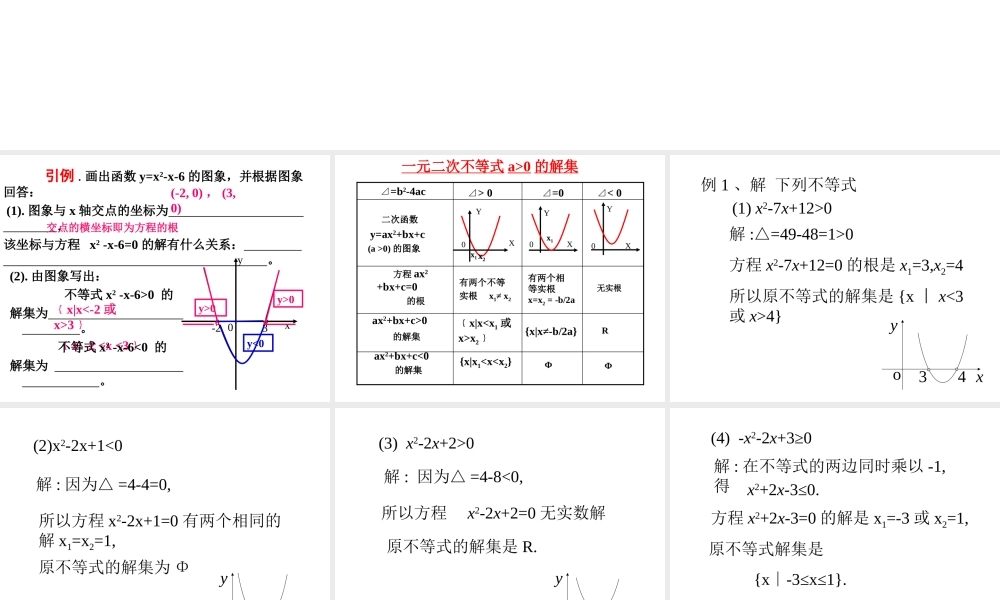
引例 . 画出函数 y=x2-x-6 的图象,并根据图象回答: (1). 图象与 x 轴交点的坐标为 ,该坐标与方程 x2 -x-6=0 的解有什么关系: 。 (-2, 0) , (3, 0) 交点的横坐标即为方程的根﹛x|x<-2 或x>3﹜﹛x| -2 0y>0y<0(2). 由图象写出: 不等式 x2 -x-6>0 的解集为 。 不等式 x2 -x-6<0 的解集为 。 一元二次不等式 a>0 的解集⊿=b2-4ac⊿> 0⊿=0 ⊿< 0 二次函数 y=ax2+bx+c (a >0) 的图象 方程 ax2+bx+c=0 的根ax2+bx+c>0 的解集 ax2+bx+c<0 的解集有两个不等实根 x1≠ x2有两个相等实根x=x2 = -b/2a无实根﹛x|xx2﹜{x|x≠-b/2a}R{x|x10△方程 x2-7x+12=0 的根是 x1=3,x2=4所以原不等式的解集是 {x ︱ x<3或 x>4}o34yx(1) x2-7x+12>0 (2)x2-2x+1<0解 : 因为△ =4-4=0,所以方程 x2-2x+1=0 有两个相同的解 x1=x2=1,o1yx原不等式的解集为 Φ (3) x2-2x+2>0解 : 因为△ =4-8<0,所以方程 x2-2x+2=0 无实数解o1yx原不等式的解集是 R. (4) -x2-2x+3≥0解 : 在不等式的两边同时乘以 -1,得x2+2x-3≤0.方程 x2+2x-3=0 的解是 x1=-3 或 x2=1,原不等式解集是 {x-3≤x≤1}.∣ 解一元二次不等式的一般步骤:( 1 )将二次项系数化为“ +” ( a>0); ( 2 )计算△判断方程是否有根;或观察能否因式分解;( 3 )如果有根,找出方程的根;( 4 )看图说话。 练习 :求下列不等式的解集(1) x2-5x+6<0 ; (2) 3x2-x-4>0 ;(3) 2x2+4x+3>0 ; ( 4 ) 9x2-6x+1≤0(5) -6x2-x+2<0 ; 比一比 , 赛一赛:( 1 ) (x-1)(x-3)>0 的解集是 .(2) x2<9 的解集是 .(3) x2-3x-4≥0 的解集是 .(4) (x-1)(2-x) ≥0 的解集是 .{x∣x<1 或 x>3}{x 1≤ ∣x≤ 2 }{x∣x≤-1 或 x≥4}{x -3<∣x<3 }(5) (x-1)2≤0 的解集是 .{1} 260{ | 23},,.axbxxxa b 已知不等式的解集是求的值想一想:解 : 由题意得 ,a<0, 且方程 ax2+bx+6=0的两根分别为 -2 和 3, 则01,66abaa所以.a =b-1=1解得 已知不等式 x2-2x+k2-1>0 解集是 R, 求实数 k 的取值范围 .变一变 解 : 由题意得△ =4-4(k2-1)<0,22.kk 或即 k2>2,解得 一元二次不等式一元二次方程二次函数关 键 :课堂小结思想方法 : 数形结合分类讨论化归 作业课本 P71 习题 1 , 2.