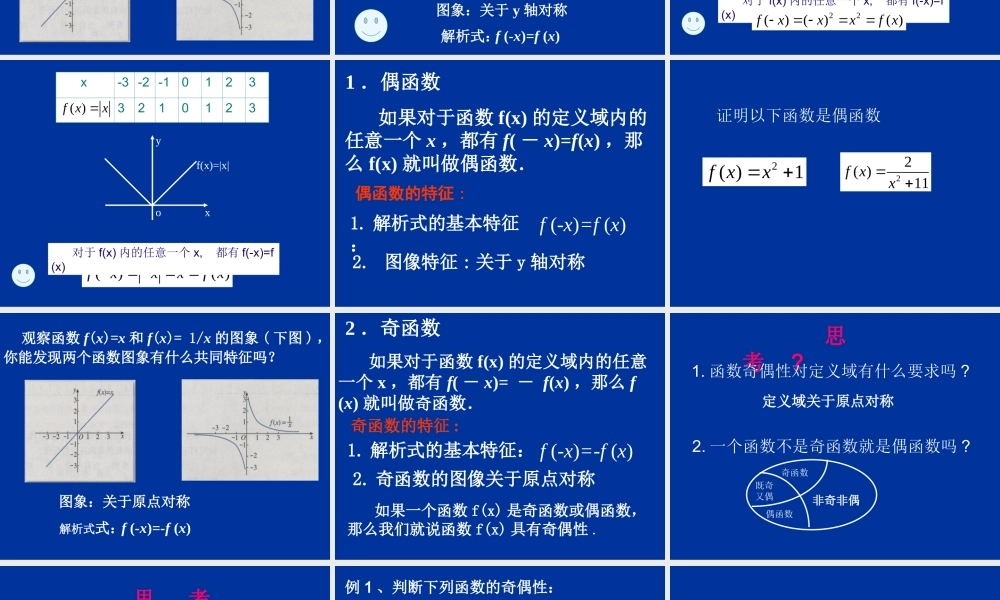
xy0 2(1)(2)||1(3)(4)f xxf xxf xxf xx 请在不同坐标系上画出以下图象,并根据对称性进行分类 . xyof(x)=x2xyof(x)=|x| 观察下图,思考并讨论以下问题:(1) 这两个函数图象有什么共同特征吗?(2) 从解析式上如何体现上述特征?xyof(x)=|x|图象:关于 y 轴对称解析式:f (-x)=f (x)xyof(x)=x2 x-3-2-1012394101492( )f xxxyof(x)=x2 对于 f(x) 内的任意一个 x, 都有 f(-x)=f(x)22()()( )fxxxf x xyof(x)=|x| x -3 -2 -101233210123( )f xx()( )fxxxf x 对于 f(x) 内的任意一个 x, 都有 f(-x)=f(x) 如果对于函数 f(x) 的定义域内的任意一个 x ,都有 f( - x)=f(x) ,那么 f(x) 就叫做偶函数. 1 .偶函数偶函数的特征 :1. 解析式的基本特征:f (-x)=f (x)2. 图像特征 : 关于 y 轴对称 2( )1f xx22( )11f xx证明以下函数是偶函数 观察函数 f(x)=x 和 f(x)= 1/x 的图象 ( 下图 ) ,你能发现两个函数图象有什么共同特征吗?图象:关于原点对称解析式式: f (-x)=-f (x) 如果对于函数 f(x) 的定义域内的任意一个 x ,都有 f( - x)= - f(x) ,那么 f(x) 就叫做奇函数. 2 .奇函数奇函数的特征 :1. 解析式的基本特征:2. 奇函数的图像关于原点对称f (-x)=-f (x) 如果一个函数 f(x) 是奇函数或偶函数,那么我们就说函数 f(x) 具有奇偶性 . 思 考 ? 1. 函数奇偶性对定义域有什么要求吗 ? 2. 一个函数不是奇函数就是偶函数吗 ? 定义域关于原点对称非奇非偶奇函数既奇又偶偶函数 思 考 ?2. 请列举一个既是奇函数又是偶函数的函数 ?1. 请列举一个既不是奇函数又不是偶函数的函数 ? (1) 先求定义域,看是否关于原点对称;例 1 、判断下列函数的奇偶性:4(1) ( ) f xx2 (3) ( ),[ 1,2]f xxx 3 (2) ( )f xx用定义判断函数奇偶性的步骤:(1) 先求定义域,看是否关于原点对称;(2) 再判断 f(-x)=-f(x) 或 f(-x)=f(x) 是否恒成立 .定义域关于原点对称是函数为偶函数或奇函数的前提条件。(3) 根据定义,作出结论 注: 而函数的奇偶性是函数的整体性质;函数的单调性是函数的局部性质 . 21(1) ( ) xf xx判断下列函数的奇偶性:课堂练习 :(3) ( )1 f xx (5) ( )0f x 3 (2) ( )2f xxx...