高二数学二元一次不等式表示的平面区域课件 人教版 课件VIP免费

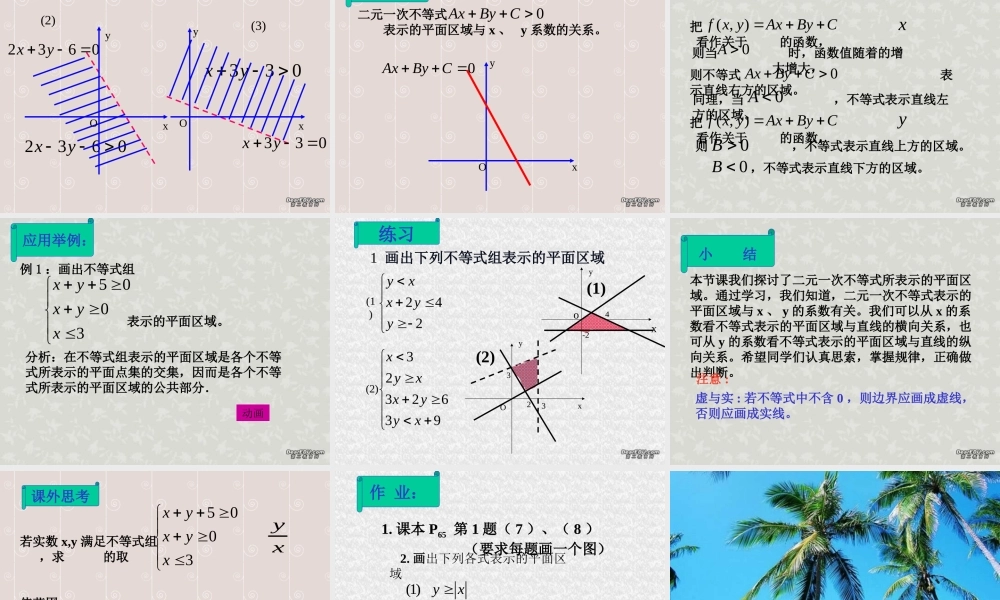
课题 : 二元一次不等式表示的区域【引入新课】在平面直角坐标系下可做出这些直线，以这些方程为坐标的点都分布在这一条条直线上。问题一请你说出所得到的式子具有的共同特征？二元一次方程我们在哪学习过二元一次方程？思：直线的方程( , )0,1,2,3, 1, 2, 3f x y 令设 ，( , )1f x yxy 我们在平面直角坐标系下作出这些直线。观察它们之间的关系及相对位置。10xyOxy111 1xy12xy13xy11xy12xy13xy这个不等式中含有两个未知数，并且未知数的次数都是一次 , 这样的不等式叫做二元一次不等式。若令 呢？( , )0f x y 我们会得到一个不等式10xy二一次不等式及其解的定义含有两个未知数，并且未知数的次数都是一次的不等式叫做二元一次不等式，使不等式成立的未知数的值叫做它的解，例如 x+y-1 ＞ 0 就是一个二元一次不等式，它的解是一些数对 (x,y) 。那么，以这个二元一次不等式的解为坐标的点在平面直角坐标下的分布情况如何呢？这就是我们这一节课要解决的问题。新课：【二元一次不等式表示的平面区域】以二元一次不等式的解为坐标的点的集合所表示的平面图形 , 叫做二元一次不等式表示的平面区域。观察上面所得方程对应直线的分布。 概念 :我们先看所得到的方程 ，( , )0f x y 观察它所表示的直线，(1,0)(0,1)是过 、 两点的直线 。l在平面直角坐标系中，所有点被直线 分成三类：l① 在直线 上；l② 在直线 的右上方的平面区域；l③ 在直线 的左下方的平面区域。10xyOxy方程 、 所表示的直线都位于直线 的上方，1 1xy12xyl可以看到 :11xy 12xy l而方程 、 所表示的直线则位于直线 的下方。由上面的数学事实，你能否得出关于不等式 表示平面区域的一个结论？10xy猜想：不等式 表示直线 上方的平面区域，而不等式 则表示直线 下方的平面区域。10xy10xy10xy10xy想一想，议一议问题二2 、在与 y 轴平行的直线上的点，横坐标相等。随着点的位置向上移动，点的纵坐标逐渐增大，此时我们可把原函数看做为 y 的函数，随着 y 的增大，函数值可增大可减小，这取决于 y 的系数的正负。1 、在与直线平行的直线上的点所对应的函数值相等；我们可从以下两方面来考虑：如何验证猜想？学生讨论问题三试根据刚才我们验证结果的方法，尝试得出...