高三数学焦点访谈 人教版 课件VIP免费

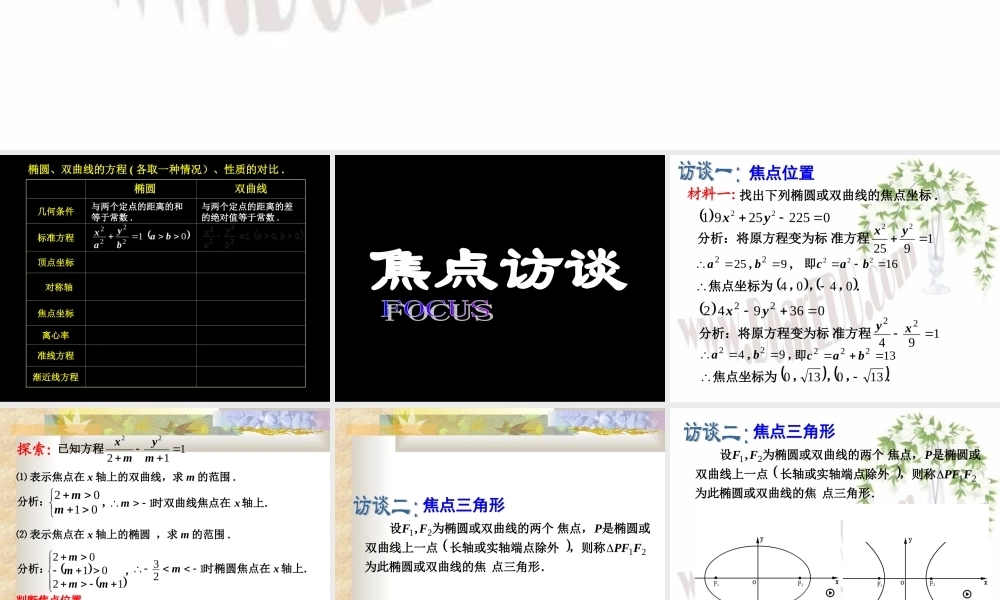
.F2F1yox.xF1F20y.. 椭圆、双曲线的方程 ( 各取一种情况）、性质的对比 . 椭圆双曲线几何条件标准方程顶点坐标 对称轴焦点坐标 离心率准线方程渐近线方程与两个定点的距离的和等于常数 .与两个定点的距离的差的绝对值等于常数 . ba,,,000,abyax22短轴长轴，长轴长轴，byax22虚轴长轴，实轴长轴，220bacc,,220bacc,,10 e1ecax2cax2xaby 焦点访谈找出下列椭圆或双曲线的焦点坐标 . 0225259122yx192522 yx准方程分析：将原方程变为标,,92522ba16222bac即 .0404，，，焦点坐标为 03694222yx材料一：焦点位置19422 xy准方程分析：将原方程变为标,,9422ba13222bac即 .130130，，，焦点坐标为 11222mymx已知方程⑴ 表示焦点在 x 轴上的双曲线，求 m 的范围 .分析：,0102mm.轴上时双曲线焦点在 xm1⑵ 表示焦点在 x 轴上的椭圆 ，求 m 的范围 .分析： ,120102mmmm.轴上时椭圆焦点在 xm123判断焦点位置.,的系数化为标准方程，观察22 yx共同点：差异：椭圆看大小，双曲线看符号 .探索： .,点三角形为此椭圆或双曲线的焦，则称长轴或实轴端点除外双曲线上一点是椭圆或焦点，为椭圆或双曲线的两个设2121FPFPFF焦点三角形.,点三角形为此椭圆或双曲线的焦，则称长轴或实轴端点除外双曲线上一点是椭圆或焦点，为椭圆或双曲线的两个设2121FPFPFF焦点三角形 .____212122214812449PFFPFPFPyxFF，则椭圆上且满足在的两个焦点，是椭圆，已知材料二：xF1F20y..P..____21212221601169PFPFPFFPyxFF，则双曲线上且满足在的两个焦点，是双曲线，已知类比：6490y..F2F1oxP.，，设长轴端点除外是椭圆上一点焦点，的两个是椭圆，已知2122222101PFFPbabyaxFF)(探索：类比：,)(,实轴端点除外是双曲线上一点的两个焦点，是双曲线，已知PbabyaxFF001222221cos12 2bcos12 2b共同点：.中利用余弦定理求解都是在21FPF差异：；椭圆aPFPF221.aPFPF221双曲线.____________21PFPF则._________2121PFPFPFF，则设xF1F20y..P. 焦点弦材料三：.的长两点，求弦、交椭圆于的右焦点，过椭圆的直线已知斜率为ABBAyxl1212...