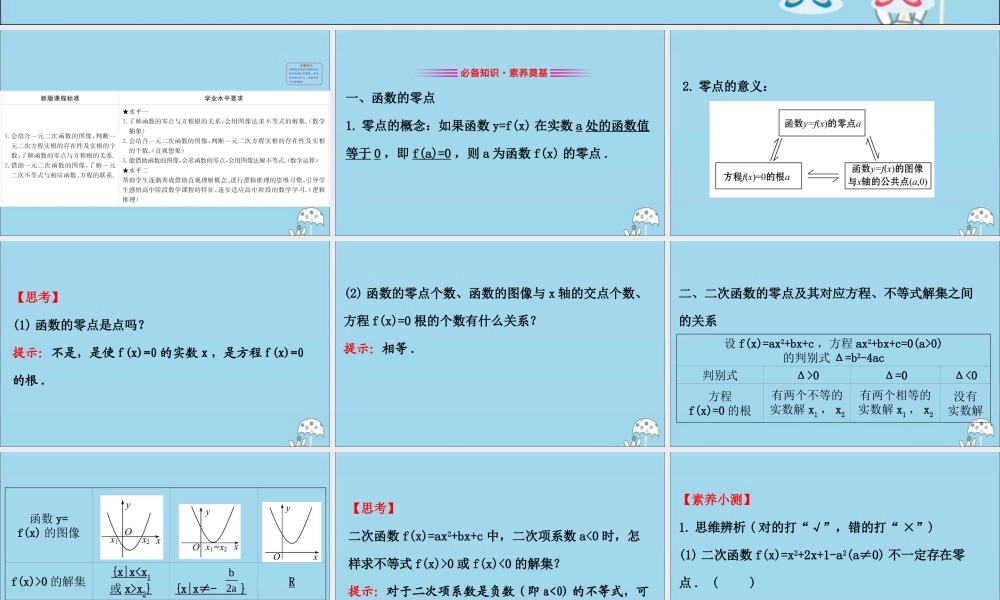
3.2 函数与方程、不等式之间的关系第 1 课时 函数的零点、二次函数的零点及其与对应方程、不等式解集之间的关系 一、函数的零点1. 零点的概念:如果函数 y=f(x) 在实数 a 处的函数值等于 0 ,即 f(a)=0 ,则 a 为函数 f(x) 的零点 .2. 零点的意义:【思考】(1) 函数的零点是点吗?提示:不是,是使 f(x)=0 的实数 x ,是方程 f(x)=0的根 .(2) 函数的零点个数、函数的图像与 x 轴的交点个数、方程 f(x)=0 根的个数有什么关系?提示:相等 .二、二次函数的零点及其对应方程、不等式解集之间的关系设 f(x)=ax2+bx+c ,方程 ax2+bx+c=0(a>0)的判别式 Δ=b2-4ac判别式Δ>0Δ=0Δ<0方程f(x)=0 的根有两个不等的实数解 x1 , x2有两个相等的实数解 x1 , x2没有实数解函数 y=f(x) 的图像 f(x)>0 的解集{x|xx2}{x|x≠- } Rf(x)<0 的解集{x|x10 或 f(x)<0 的解集?提示:对于二次项系数是负数 ( 即 a<0) 的不等式,可以先把二次项系数化成正数,再求解;也可以画出二次项系数为负数时的函数图像,再求解 .【素养小测】1. 思维辨析 ( 对的打“√”,错的打“ ×”)(1) 二次函数 f(x)=x2+2x+1-a2(a≠0) 不一定存在零点 .( )(2) 若 a>0 ,则一元二次不等式 ax2+1>0 无解 . ( )(3) 若一元二次方程 ax2+bx+c=0 的两根为x1 , x2(x10 ,所以函数有两个零点 .(2)×. 因为 a>0 ,所以不等式 ax2+1>0 恒成立,即原不等式的解集为 R.(3)×. 当 a>0 时, ax2+bx+c<0 的解集为 {x|x12x 的解集是( )A.{x|x≥5 或 x≤-1}B.{x|x>5 或 x<-1}C.{x|-12x ,得 x2-4x-5>0 ,因为 x2-4x-5=0 的两根为 -1 , 5 ,故 x2-4x-5>0 的解集为 {x|x<-1 或 x>5}.3. 不等式 9x2+6x+1≤0 的解集是( )111A.{x|x}B.{x|x}3331C.D.{x|x}3 【解析】选 D. 不等式可化为 (3x+1)2≤0 ,因此只有 x=- ,即解集为 1{x|x}.313类型...