相似三角形九年级数学课件 华东师大版 课件VIP免费

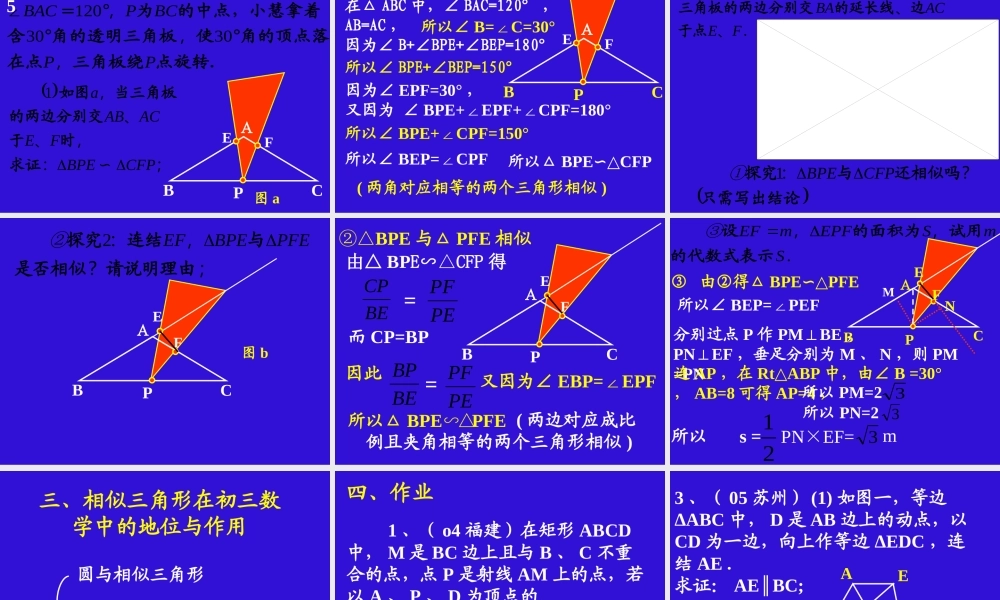
相似三角形 一、课改实验区中考试题点旋转．三角板绕在点角的顶点落使角的透明三角板含的中点，小慧拿着为中，等腰PPBCPBACACABABC，，，， °°°===3030120∠8 ；：，、、，CFPBPEFEACABa∽1求证时于的两边分别交当三角板如图ＡBCEFP图 a  ．、、，：２FEACBAbP于点边的延长线三角板的两边分别交情形时旋转到图将三角板绕点操作只需写出结论还相似吗与探究？：CFPBPE①1 ．，，SmSEPFmEF③的代数式表示试用的面积为设；？，：请说明理由是否相似与连结探究PFEBPEEF②2ＡBCEFP图 b (2) 性质两个三角形相似，则 ③ 它们的周长比等于相似比；面积比等于相似比的平方． ① 它们的对应边成比例，对应角相等； ② 它们的对应高、对应中线、对应角平分线的比等于相似比； (4) 应用举例例 1 判断① 所有的等腰三角形都相似．② 所有的直角三角形都相似．③ 所有的等边三角形都相似．④ 所有的等腰直角三角形都相似．(×)(√)(√)(×) 2323，Ryx xyP6322，，，得由反比例函数()yxR，设时当AOCBRT①∽yxRTBTOCAO22421131132113113，Ryx时当CAOBRT②∽224xyBTRTOCAO 例 3 在方格纸中，每个小格的顶点称为格点，以格点的连线为边的三角形称为格点三角形，如图所示的 5×5 的方格纸中，如果想作格点 ΔABC 与 ΔOAB 相似 ( 相似比不能为 1) ，则 C 点坐标为____________ ．OxABy OxABy125C1(5 ， 2)55252C2(4 ， 4) (1) 操作：请你在如图所示的黄金矩形 ABCD(AB>CD) 中 , 以短边 AD 为一边作正方形 AEFD;ABCDEF例 4 (05 年扬州市中考题 ) 若一个矩形的短边与长边的比值为 ( 黄金分割数 ) ，我们把这样的矩形叫做黄金矩形．21-5 ABCDEF (2) 探究：在 (1) 中的四边形EBCF 是不是黄金矩形？若是，请予以证明；若不是，请说明理由；四边形 EBCF 是矩形，而且是黄金矩形 是矩形四边形是矩形四边形是正方形四边形EBCFCBBEFCBABCDBEFAEFAEFD90909090，，，ABCDEF21511521babbaEFCF215 abbADaCD则设，，∴ 矩形 EBCF 是黄金矩形 (3) 归纳：通过上述操作及探究，请概括出具有一般性的结论( 不需要证明 ) ． 在黄金矩形内以短边为边作一个正方形后，所得到的另一个四边形是...