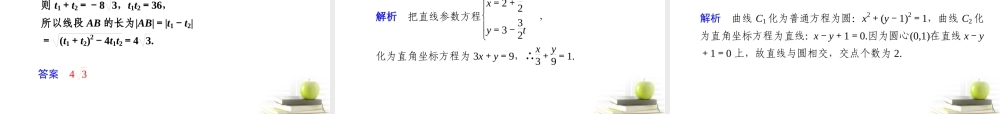§2 坐标系与参数方程 真题热身 1.(2011·陕西)在直角坐标系 xOy 中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,设点 A,B 分别在曲线 C1: x=3+cos θ,y=4+sin θ(θ 为参数)和曲线 C2:ρ=1 上,则 AB 的最小值为________. 解析 C1:(x-3)2+(y-4)2=1,C2:x2+y2=1, ∴两圆心之间的距离为 d= 32+42=5. A∈曲线 C1,B∈曲线 C2,∴(|AB|)min=5-2=3. 3 2.(2010·广东)在极坐标系(ρ,θ)(0≤θ<2π)中,曲线 ρ=2sin θ 与 ρcos θ=-1 的交点的极坐标为________. 解析 曲线 ρ=2sin θ 化为直角坐标系方程为 x2+y2-2y=0. 由 ρcos θ=-1 可化为 x=-1.将 x=-1 代入 x2+y2-2y=0 得 x=-1,y=1,因此交点的直角坐标为(-1,1),化为极坐 标为2,3π4 . 2,3π4 考点整合 1.直角坐标与极坐标的互化 把直角坐标系的原点作为极点,x 轴正半 轴作为极轴,且在两坐标系中取相同的长 度单位. 设 M 是平面内的任意一点,它 的直角坐标、极坐标分别为(x,y)和(ρ,θ), 则 x=ρcos θy=ρsin θ, ρ2=x2+y2tan θ=yx(x≠0). 2.直线的极坐标方程 若直线过点 M(ρ0,θ0),且极轴到此直线的角为 α,则它的方程为:ρsin(θ-α)=ρ0sin(θ0-α). 几个特殊位置的直线的极坐标方程 (1)直线过极点:θ=θ0 和 θ=π-θ0; (2)直线过点 M(a,0)且垂直于极轴:ρcos θ=a; (3)直线过 M(b,π2)且平行于极轴:ρsin θ=b. 3.圆的极坐标方程 若圆心为 M(ρ0,θ0),半径为 r 的圆方程为:ρ2-2ρ0ρcos(θ -θ0)+ -r2=0. 几个特殊位置的圆的极坐标方程 (1)当圆心位于极点,半径为 r:ρ=r; (2)当圆心位于 M(r,0) ,半径为 r:ρ=2rcos θ; (3)当圆心位于 M(r,π2),半径为 r:ρ=2rsin θ. 204.直线的参数方程 过定点 M(x0,y0),倾斜角为 α 的直线 l 的参数方程为 x=x0+tcos α,y=y0+tsin α(t 为参数). 5.圆的参数方程 圆心在点 M(x0,y0),半径为 r 的圆的参数方程为 x=x0+rcos θ,y=y0+rsin θ(θ 为参数,0≤θ≤2π). 6.圆锥曲线的参数方程 (1)椭圆x2a2+y2b2=1 的参数方程为 x=acos θy=bsin θ(θ 为参数). (2)双曲线x2...