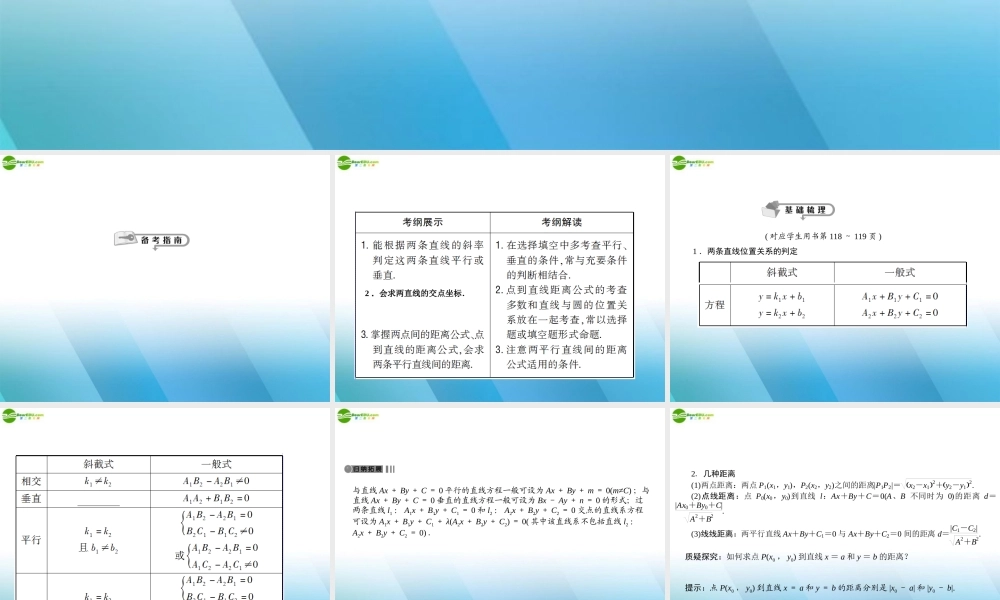
第 2 节 两直线的位置关系2 .会求两直线的交点坐标.( 对应学生用书第 118 ~ 119 页 )1 .两条直线位置关系的判定与直线 Ax + By + C = 0 平行的直线方程一般可设为 Ax + By + m = 0(m≠C) ;与直线 Ax + By + C = 0 垂直的直线方程一般可设为 Bx - Ay + n = 0 的形式;过两条直线 l1 : A1x + B1y + C1 = 0 和 l2 : A2x + B2y + C2 = 0 交点的直线系方程可设为 A1x + B1y + C1 + λ(A2x + B2y + C2) = 0( 其中该直线系不包括直线 l2 :A2x + B2y + C2 = 0) .2.几种距离 (1)两点距离:两点 P1(x1,y1),P2(x2,y2)之间的距离|P1P2|= x2-x12+y2-y12. (2)点线距离:点 P0(x0,y0)到直线 l:Ax+By+C=0(A、B 不同时为 0)的距离 d=|Ax0+By0+C|A2+B2. (3)线线距离:两平行直线 Ax+By+C1=0 与 Ax+By+C2=0 间的距离 d=|C1-C2|A2+B2. 质疑探究:如何求点 P(x0 , y0) 到直线 x = a 和 y = b 的距离?提示:点 P(x0 , y0) 到直线 x = a 和 y = b 的距离分别是 |x0 - a| 和 |y0 - b|.1 . (2010 年高考安徽卷 ) 过点 (1,0) 且与直线 x - 2y - 2 = 0 平行的直线方程是( A )(A)x - 2y - 1 = 0 (B)x - 2y + 1 = 0(C)2x + y - 2 = 0 (D)x + 2y - 1 = 0解析:与直线 x - 2y - 2 = 0 平行的直线方程可设为: x - 2y + c = 0(c≠ -2) ,将点 (1,0) 代入 x - 2y + c = 0 ,解得 c =- 1 ,故直线方程为 x - 2y -1 = 0 ,选 A.2 .若三条直线 y = 2x , x + y = 3 , mx + ny + 5 = 0 相交于同一点,则点 (m ,n) 可能是 ( A )(A)(1 ,- 3) (B)(3 ,- 1)(C)( - 3,1) (D)( - 1,3)解析:由 y=2x,x+y=3, 得 x=1,y=2, ∴由题意知 m+2n+5=0,∴点(m,n)可能是(1,-3). 3.已知点(a,2)(a>0)到直线 l:x-y+3=0 的距离为 1,则 a 等于( C ) (A)2 (B)2- 2 (C)2-1 (D) 2+1 解析:由题意知|a-2+3|2=1, 解之得 a=- 2-1(舍去)或 a= 2-1.故应选 C. 4 .已知直线 l1 与 l2 : x + y - 1 = 0 平行,且 l1...