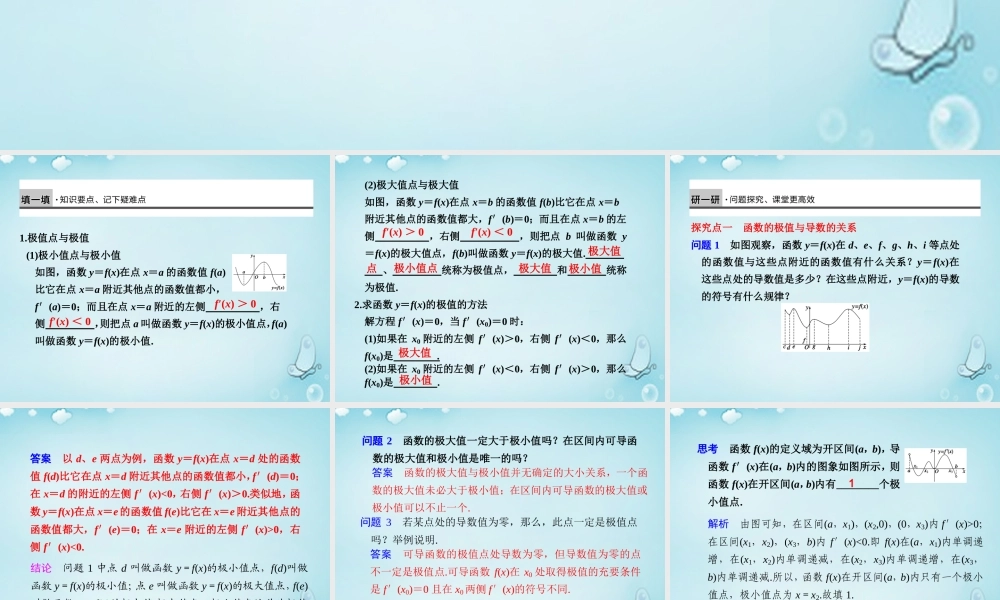
1.极值点与极值 (1)极小值点与极小值 如图,函数 y=f(x)在点 x=a 的函数值 f(a) 比它在点 x=a 附近其他点的函数值都小, f′(a)=0;而且在点 x=a 附近的左侧 ,右 侧 ,则把点 a 叫做函数 y=f(x)的极小值点,f(a) 叫做函数 y=f(x)的极小值. f′(x) < 0 f′(x) > 0 (2)极大值点与极大值 如图,函数 y=f(x)在点 x=b 的函数值 f(b)比它在点 x=b 附近其他点的函数值都大,f′(b)=0;而且在点 x=b 的左侧 ,右侧 ,则把点 b 叫做函数 y=f(x)的极大值点,f(b)叫做函数 y=f(x)的极大值. 、 统称为极值点, 和 统称为极值. 2.求函数 y=f(x)的极值的方法 解方程 f′(x)=0,当 f′(x0)=0 时: (1)如果在 x0 附近的左侧 f′(x)>0,右侧 f′(x)<0,那么f(x0)是 . (2)如果在 x0 附近的左侧 f′(x)<0,右侧 f′(x)>0,那么f(x0)是 . f′(x) > 0 f′(x) < 0 极大值 点 极小值点 极大值 极小值 极大值极小值探究点一 函数的极值与导数的关系 问题 1 如图观察,函数 y=f(x)在 d、e、f、g、h、i 等点处的函数值与这些点附近的函数值有什么关系?y=f(x)在这些点处的导数值是多少?在这些点附近,y=f(x)的导数的符号有什么规律? 答案 以 d、e 两点为例,函数 y=f(x)在点 x=d 处的函数值 f(d)比它在点 x=d 附近其他点的函数值都小,f′(d)=0;在 x=d 的附近的左侧 f′(x)<0,右侧 f′(x)>0.类似地,函数 y=f(x)在点 x=e 的函数值 f(e)比它在 x=e 附近其他点的函数值都大,f′(e)=0;在 x=e 附近的左侧 f′(x)>0,右侧 f′(x)<0. 结论 问题 1 中点 d 叫做函数 y=f(x)的极小值点,f(d)叫做函数 y=f(x)的极小值;点 e 叫做函数 y=f(x)的极大值点,f(e)叫做函数 y=f(x)的极大值.极大值点、极小值点统称为极值点,极大值和极小值统称为极值. 问题 2 函数的极大值一定大于极小值吗?在区间内可导函数的极大值和极小值是唯一的吗? 答案 函数的极大值与极小值并无确定的大小关系,一个函数的极大值未必大于极小值;在区间内可导函数的极大值或极小值可以不止一个. 问题 3 若某点处的导数值为零,那么,此点一定是极值点吗?举例说明. 答案 可导函数的极值点处导数为零,但导数值为零的点不一定是极值点.可导函数 f(x)在 x0 处取得极值的充要条件是 f′(x0)=0 且在 x0 两侧 f′(x)的...