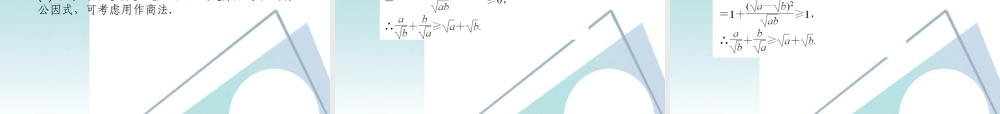• ● 基础知识• 一、比较法• 比较法是证明不等式的最基本、最重要的方法之一,它可分为 、 .• 1 .作差法• ① 理论依据: a>b⇔ ;• a0a - b<0a - b = 0作差变形判断符号•2 .作商法•① 要证 A>B(B>0) ,只要证 ; •要证 A0) ,只要证 . •② 证明步骤: ―→ ―→ .•常用变形方法:一是配方法,二是分解因式.作商变形判断与 1 的关系• 二、分析法• 从求证的不等式出发,逐步寻求使不等式成立的• ,直至所需条件被确认成立,就断定求证的不等式成立,这种证明方法叫分析法.分析法的思想“是• ” :即从求证的不等式出发,探求使结论成立的充分条件,直至已成立的不等式.•“采用分析法证明不等式时,常用 ”的符号,有“时,若为充要条件时,也常用 ”的符号.证明“…………”过程常表示为 要证只要证.充分条件执果索因⇐⇔• 三、综合法• 所谓综合法,就是从 和已经证明过的基本不等式和不等式的 推导出所要证明的不等式成立,可简称为 .• 在使用综合法证明不等式时,要注意基本不等式的应用.题设条件由因导果性质•常用的基本不等式有:•(1) 若 a , b∈R ,则 a2 0 , |a| 0 , (a±b)2 0 , a2±2ab+ b2 0.•(2) 若 a , b∈R ,则 a2+ b2 2ab( 当且仅当 时取等号 ) , ≥ ab( 当且仅当 时取等号 ) ;若 a + b > 0 ,且ab≠0 ,则 ( 当且仅当 a = b 时取等号 ) ; a2+ b2+ c2≥ ( 当且仅当 时取等号 ) 等. ≥≥≥≥≥a = ba = b≥ab + bc + aca = b = c• (3) 若 a , b∈R +,则 ≤ • (4) 若 ab > 0 ,则 2. • (5)||a| - |b||≤ ≤ .• 应用上述基本不等式时,一要注意条件 ;二要注意不等式 的条件.• 常用不等式:若 a , b , m > 0 ,且 a < b ,≥|a±b||a| + |b|a , b 的符号等号成立• ● 易错知识• 不等式的性质用错.• 1 . a 、 b 是正数,求证: • 解题思路:• 注:错解: a2+ b2≥2ab , a + b≥2 • ● 回归教材• 1 .若 a > b , m > 0 ,则下列不等式恒成立的是( )• A . (a + m)2> (b + m)2• C . (a - m)3 > (b - m)3• D . ...