高二数学空间向量的基本定理课件 苏教版 课件VIP免费

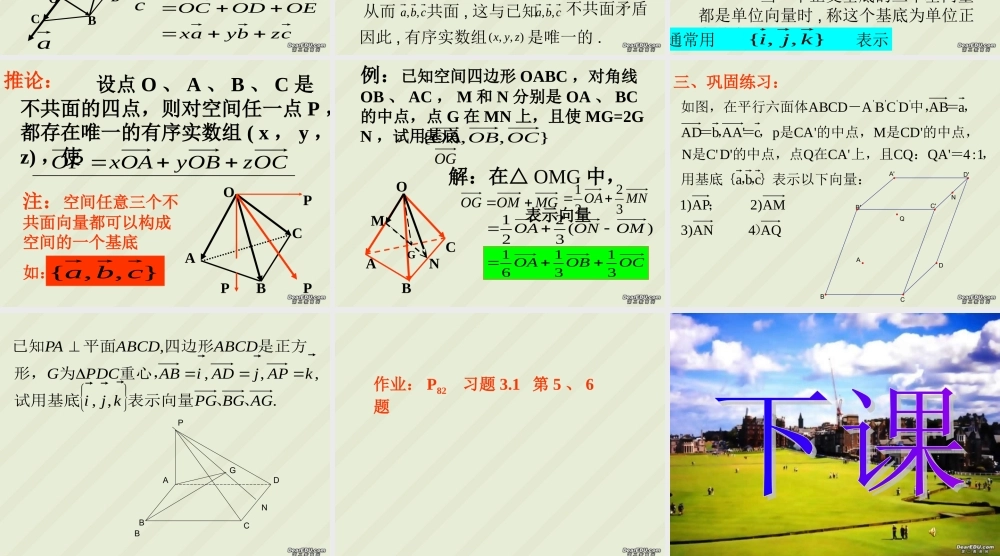
一、复习平面向量的基本定理2211eteta如果 ， 是平面内两个不共线向量，那么对于这一平面内的任一向量 ，有且只有一对实数 t1 ， t2 ，使 1e2eaOCMN1e2eaONOMOC2211etet对向量 进行分解：a空间任一向量能用三个不共面的向量来线性表示吗？POxyz二、空间向量的基本定理：如果三个向量 不共面，那么对空间任一向量 ，存在一个唯一的有序实数组 (x ，y ， z) ，使cba,,pczbyaxpABDCOabc思路：作cBCaBDbAB//,//,//czbyaxOEODOCBAOBppE下证唯一性 :假设存在实数组),,(zyx,且xx , 使czbyaxp那么即czbyaxczbyax0)()()(czzbyyaxx因为所以xxcxxzzbxxyya从而cba,,共面 , 这与已知cba,,不共面矛盾因此 , 有序实数组),,(zyx是唯一的 . 如果三个向量 不共面 , 那么空间的每一个向量都可由向量 线性表示 . 把 称为空间的一个基底321,,eee321,,eee},,{321eee基底 :基向量 : 如果空间一个基底的三个向量是两两互相垂直 , 那么这个基底叫做正交基底 . 321,,eee正交基底 :单位正交基底 : 当一个正交基底的三个基向量都是单位向量时 , 称这个基底为单位正交基底 . 通常用 表示},,{kji 设点 O 、 A 、 B 、 C 是不共面的四点，则对空间任一点 P ，都存在唯一的有序实数组 ( x ， y ，z) ，使OCzOByOAxOPOABCPPP注：空间任意三个不共面向量都可以构成空间的一个基底如：},,{cba推论：例：已知空间四边形 OABC ，对角线OB 、 AC ， M 和 N 分别是 OA 、 BC的中点，点 G 在 MN 上，且使 MG=2GN ，试用基底 表示向量},,{OCOBOAOGOABCMNG解：在△ OMG 中，MGOMOGMNOA3221)(3221OMONOAOCOBOA313161AQ4 AN3)AM2) AP1)cba1:4QA'CQCA'QD'C'N'CDM'CApcAA'bADaABDCBAABCD''''）；｝表示以下向量：，，用基底｛，＝：上，且在的中点，点是的中点，是的中点，是，＝，＝，＝中，－如图，在平行六面体B'CDAA'C'D'BQN三、巩固练习：PABBCDNG.,,,,,,AGBGPGkjikAPjADiABPDCGABCDABCDPA、、表示向量试用基底重心，为形，是正方四边形平面已知作业： P82 习题 3.1 第 5 、 6题