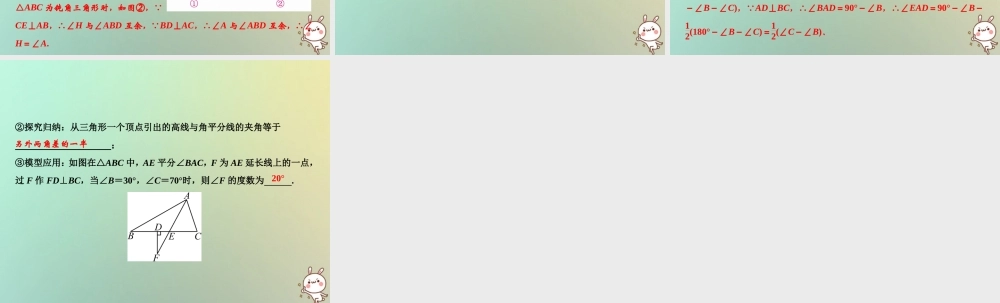
第十一章 三角形专题强化二 探索与三角形有关的夹角2018 秋季数学 八年级 上册• R 强化角度 1 求三角形内外角平分线的夹角 1.如图,在△ABC 中,∠ABC 的平分线与∠ACB 的外角平分线交于点 P,∠P 与∠A有什么数量关系? ①写出探究过程: 解:∠P=12∠A.由∠2 是△BPC 的外角,得∠P+∠1=∠2.因为 BP 是∠ABC的平分线,CP 是∠ACB 的外角平分线,所以∠1=12∠ABC,∠2=12∠ACD,由∠ACD 是△ABC 的外角,得∠ACD=∠ABC+∠A,所以∠2=12(∠ABC+∠A),所以∠P=∠2-∠1=12(∠ABC+∠A)-12∠ABC=12∠A. ②探究归纳:即三角形一个内角的平分线和另一个角的外角平分线所夹的角等于 . ③模型应用:如图,在△ABC 中,若∠ABC 的平分线与∠ACB 的外角平分线交于点 D,∠A=50°,则∠D= ,若∠2 与∠1 的角平分线交于 E,则∠E= . 第三个角的一半 25° 12.5° 2.如图,在△ABC 中,∠ABC=50°,∠ACB=60°,点 E 在 BC 的延长线上,∠ABC 的平分线 BD 与∠ACE 的平分线 CD 相交于点 D,连接 AD,下列结论中不正确的是( ) A.∠BAC=70° B.∠DOC=90° C.∠BDC=35° D.∠DOA=95° B 强化角度 2 求三角形高线的夹角 3.在△ABC 中∠C≠90°,高 BD 和 CE 所在的直线交于 H,求∠BHC 与∠A 有什么关系. ①写出探究过程: 解:∠BHC+∠A=180°或∠BHC=∠A.当△ABC 为锐角三角形时,如图①, ∵CE⊥AB,∴∠ABD+∠EHB=90°,∵BD⊥AC,∴∠ABD+∠A=90°,∴∠A=∠BHE,∵∠BHC 与∠BHE 互补,∴∠BHC 与∠A 互补;当△ABC 为钝角三角形时,如图②,∵CE⊥AB,∴∠H 与∠ABD 互余,∵BD⊥AC,∴∠A 与∠ABD 互余,∴∠H=∠A. ②探究归纳:非直角三角形的两条边上高线所夹的角与第三边所对的角 ; ③模型应用:在钝角△ABC 中,∠A=45°,高 BD 和 CE 所在的直线交于点H,则∠BHC 的度数为 . 相等或互补 45° 强化角度 3 求高线与角平分线的夹角 4.如图,在△ABC 中,AE 平分∠BAC(∠B<∠C),AD⊥BC,垂足为 D.∠EAD 与∠B、∠C 有什么数量关系. ①写出探究过程: 解:∠EAD=12(∠C-∠B).∵AE 平分∠BAC,∴∠BAE=12∠BAC=12(180°-∠B-∠C),∵AD⊥BC,∴∠BAD=90°-∠B,∴∠EAD=90°-∠B-12(180°-∠B-∠C)=12(∠C-∠B). ②探究归纳:从三角形一个顶点引出的高线与角平分线的夹角等于 ; ③模型应用:如图在△ABC 中,AE 平分∠BAC,F 为 AE 延长线上的一点,过 F 作 FD⊥BC,当∠B=30°,∠C=70°时,则∠F 的度数为 . 另外两角差的一半 20°