高二数学(绝对值三角不等式)课件VIP免费

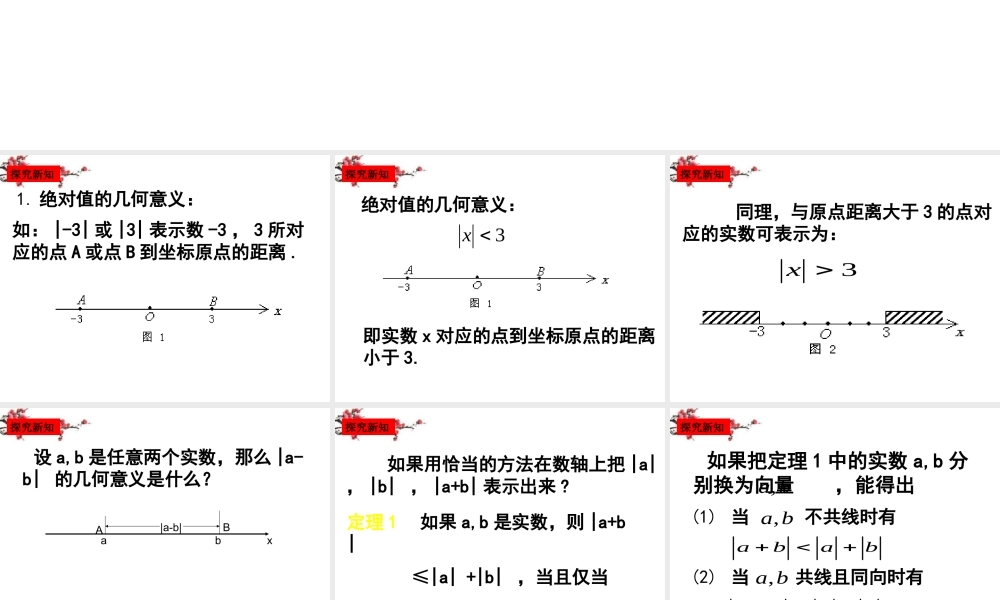
绝对值三角不等式 1. 绝对值的几何意义： 如： |-3| 或 |3| 表示数 -3 ， 3 所对应的点 A 或点 B 到坐标原点的距离 .探究新知3x即实数 x 对应的点到坐标原点的距离小于 3.探究新知 绝对值的几何意义： 同理，与原点距离大于 3 的点对应的实数可表示为： 3x探究新知 设 a,b 是任意两个实数，那么 |a-b| 的几何意义是什么？x|a-b|abAB探究新知 如果用恰当的方法在数轴上把 |a| ， |b| ， |a+b| 表示出来 ?定理 1 如果 a,b 是实数，则 |a+b| ≤|a| +|b| ，当且仅当 ab≥0 时，等号成立 .探究新知 如果把定理 1 中的实数 a,b 分别换为向量 ，能得出,a babab(1) 当 不共线时有,a b(2) 当 共线且同向时有abab,a b探究新知abababab探究新知|a|-|b| ≤|a±b|≤|a|+|b| 这个不等式俗称“三角不等式”——三角形中两边之和大于第三边，两边之差小于第三边绝对值三角不等式求证： |a|-|b| ≤|a±b|≤|a|+|b| 定理的证明探究新知定理 2 ：如果 a,b,c 是实数，那么acabbc)()0ab bc当且仅当（时，等号成立探究新知,,5ybεεεε例1 已知 >0,x-a求 2x+3y-2a-3b典例讲评例 2 两个施工队分别被安排在公路沿线的两个地点施工 , 这两个地点分别位于公路路碑的第 10 公里和第 20 公里处 . 现要在公路沿线建两个施工队的共同临时生活区 , 每个施工队每天在生活区和施工地点之间往返一次 , 要使两个施工队每天往返的路程之和最小 , 生活区应该建于何处 ?·10x··20典例讲评解：如果生活区建于公路路碑的第 x km 处，两施工队每天往返的路程之和为 S(x)km那么 S(x)=2(|x-10|+|x-20|)-230(10)( )10(1020)230(20)xxS xxxx≤ ≤ 典例讲评10,S x所以（ ）的最小值是答 : 生活区建于两路碑间的任意位置都满足条件 .当1020x≤≤时取到. 典例讲评2040601020300xy求证 .例 3 已知 ，MyabyMax,0,20,2 abxy证明：byaaxyabyayaxyabxy.22aaMMbyaaxy典例讲评.|| 1, || 1,11ababab例4已知求证22()111(1)abababab 证明：2222212aabbaba b 222210aba b22(1)(1)0ab|| 1,||1,ab由可知22(1)(1)0ab成立，11abab所以典例讲评例 5 求证 . bbaababa111证明：在 时，显然成立 .0ba当 时，左边 0ba111ba11111abababab.11bbaa典例讲评布置作业P19 4,5