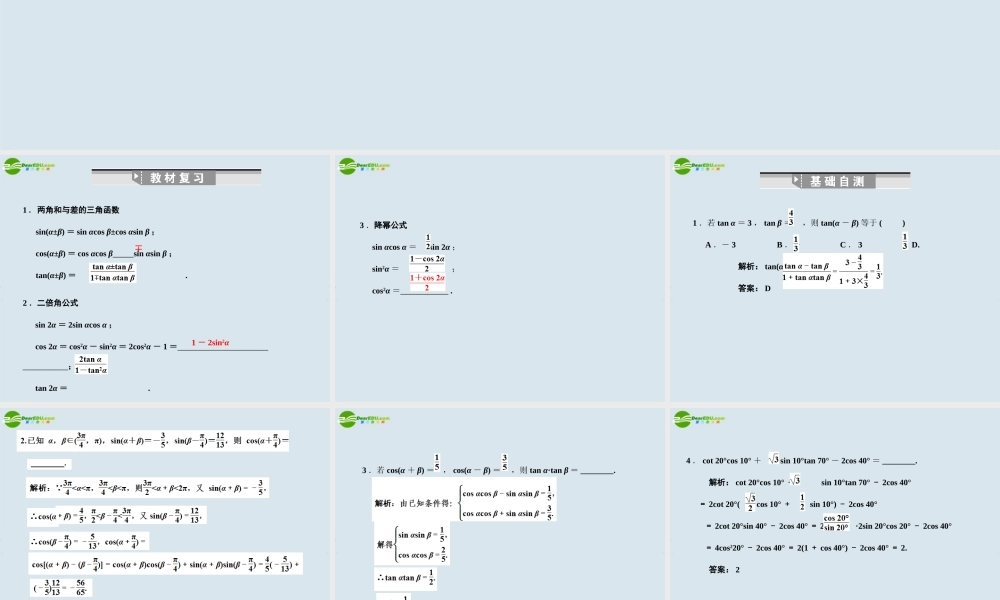
会用向量的数量积推导出两角差的余弦公式 / 能利用两角差的余弦公式导出两角差的正弦、正切公式 / 能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系3.3 两角和与差的三角函数1 .两角和与差的三角函数sin(α±β) = sin αcos β±cos αsin β ;cos(α±β) = cos αcos β sin αsin β ;tan(α±β) = .∓1 - 2sin2α2 .二倍角公式 sin 2α = 2sin αcos α ; cos 2α = cos2α - sin2α = 2cos2α - 1 = ; tan 2α = .3 .降幂公式sin αcos α =sin 2α ; sin2α =; cos2α = .1 .若 tan α = 3 , tan β =,则 tan(α - β) 等于 ( ) A .- 3 B .-C . 3 D. 解析: tan(α - β) = 答案: D3 .若 cos(α + β) =, cos(α - β) =,则 tan α·tan β = ________.4 . cot 20°cos 10° +sin 10°tan 70° - 2cos 40° = ________. 解析: cot 20°cos 10° + sin 10°tan 70° - 2cos 40°= 2cot 20°( cos 10° + sin 10°) - 2cos 40° = 2cot 20°sin 40° - 2cos 40° = 2 ·2sin 20°cos 20° - 2cos 40° = 4cos220° - 2cos 40° = 2(1 + cos 40°) - 2cos 40° = 2. 答案: 2两角和差的三角函数公式可看作是诱导公式的推广,可用 α 、 β 的三角函数表示α±β 的三角函数,在使用两角和差的三角函数公式时,特别要注意角与角之间的关系,完成统一角和角与角转换的目的.【例 1 】已知 α 为第二象限角, sin α = , β 为第一象限角, cos β = ,求 tan(2α - β) .1. 两角和、差的正切公式的变形使用如: tan α + tan β = tan(α + β)·(1 - tan αtan β) ;2 . cos αcos 2α…cos 2nα =;3 .辅助角公式 asin x + bcos x =sin(x + φ) .变式 2. 求值: (1)sin 6°sin 42°sin 66°sin 78° ; (2)(tan 10° - )sin 40°. 解答: (1) 原式= sin 6°cos 48°cos 24°cos 12° = (2) 原式= ( )·sin 40° = 1.α = (α - β) + β = (α + β) - β ;2.α =3 . 2α = (α +...