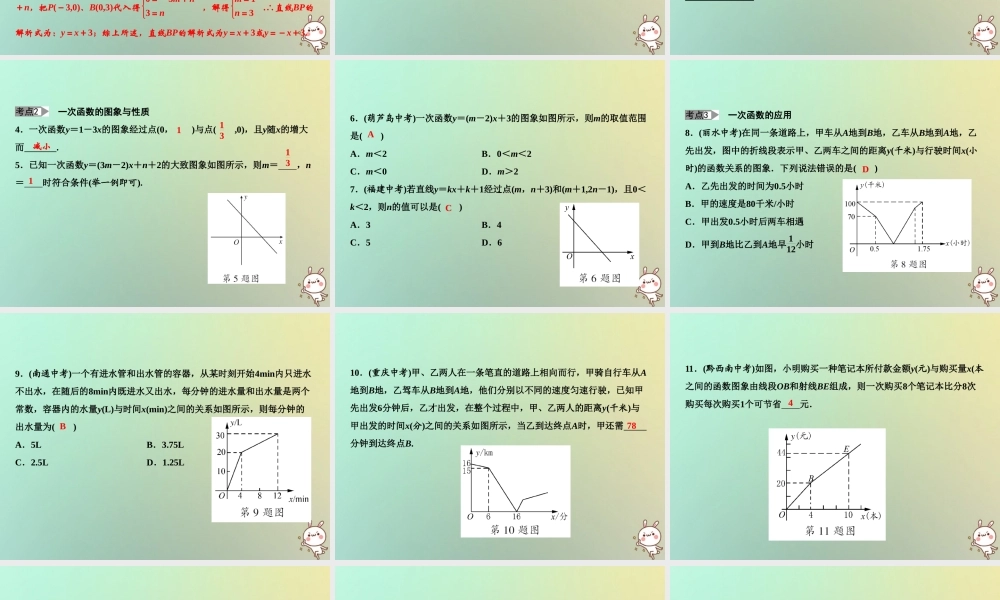
第四章 一次函数 章末小结 2018 秋季数学 八年级 上册 • B 【易错分析】 【例1】若直线y=3x+b与两坐标轴所围成的三角形的面积是6个单位,则b的值是________. 【分析】 直线y=3x+b与两坐标轴的交点为(0,b)、(- b3 ,0),则直线y=3x+b与两坐标轴围成的三角形的面积:12·|b|·|-b3|=6,求解即可. 【解答】直线y=3x+b与两坐标轴的交点为(0,b)、(- b3 ,0),则直线y=3x+b与两坐标轴所围成的三角形的面积:12·|b|·|-b3|=6,解得:b=6,b=-6,则b的值是±6.故答案为:±6. 【例2】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B. (1)求A、B两点的坐标; (2)过B点作直线BP,与x轴相交于P,且使OP=2OA,求直线BP的函数表达式. 【分析】 (1)根据坐标轴上点的坐标特征确定A点和B点的坐标;(2)由OA=32,OP=2OA得到OP=3,分类讨论:当点P在x轴正半轴上时,则P点的坐标为(3,0);当点P在x轴负半轴上时,则P点的坐标为(-3,0),然后根据待定系数法求两种情况下的直线解析式. 【解答】 (1)把x=0代入y=2x+3,得y=3,∴点B的坐标为(0,3);把y=0代入y=2x+3,得0=2x+3,解得x=- 32 ,∴点A的坐标为(- 32 ,0); (2) OA= 32 ,∴OP=2OA=3,当点P在x轴正半轴上时,则P点的坐标为(3,0),设直线BP的解析式为:y=kx+b,把P(3,0)、B(0,3)代入得 3k+b=0b=3,解得 k=-1b=3,∴直线BP的解析式为:y=-x+3;当点P在x轴负半轴上时,则P点的坐标为(-3,0),设直线BP的解析式为:y=mx+n,把P(-3,0)、B(0,3)代入得 0=-3m+n3=n,解得 m=1n=3.∴直线BP的解析式为:y=x+3;综上所述,直线BP的解析式为y=x+3或y=-x+3. 【考点强化训练】 函数的概念 1.下列关于变量x、y的关系中:①4x-3y=2 ;②y=|x|;③y= 5x ;④2x-y2=0,其中y是x的函数的是( ) A.①②③ B.①②③④ C.①③ D.①③④ A 2.已知x=3y-4,若用x来表示y,则( ) A.变量为x和y,常量仍为3和-4 B.变量不是x、y C.变量仍为x和y,常量为13和43 D.变量仍为x和y,常量为-13和-43 3.(内江中考)在函数y= 1x-3+ x-2中,自变量x的取值范围是 . C x≥2 且 x≠3 一次函数的图象与性质 4.一次函数y=1-3x的图象经过点(0, )与点( ,0),且y随x的增大而 . 5.已知一次函数y=(3m-2)x+n+2的大致图象如图所示,则...