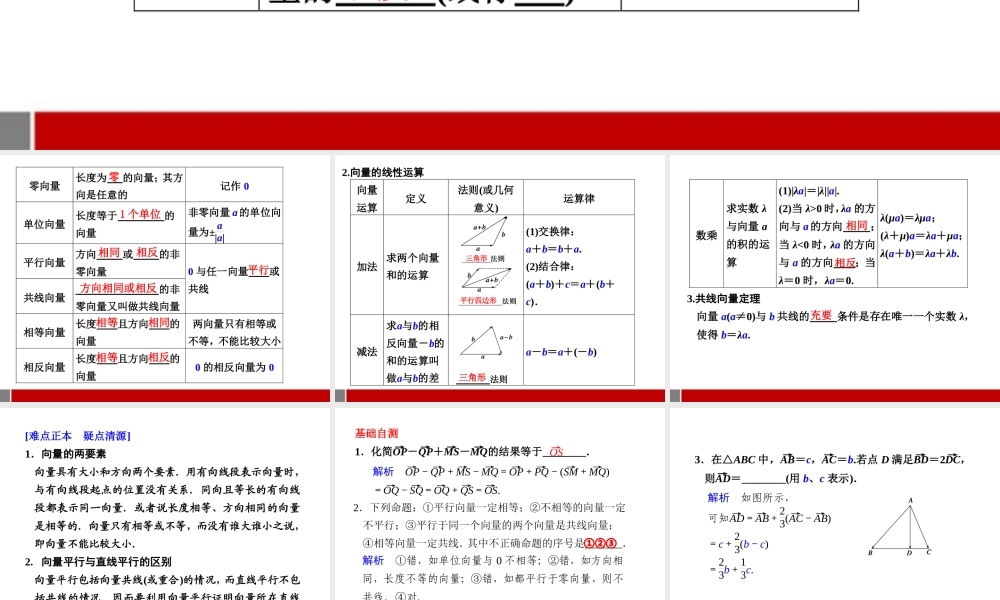
第五章 平面向量 §5.1 平面向量的概念及线性运算 基础知识 自主学习 要点梳理 1.向量的有关概念 名称 定义 备注 向量 既有 又有 的量;向量的大小叫做向量的 (或称 ) 平面向量是自由向量 大小 方向 长度 模 零向量 长度为 的向量;其方向是任意的 记作 0 单位向量 长度等于 的 向量 非零向量 a 的单位向量为± a|a| 平行向量 方向 或 的非零向量 共线向量 的非零向量又叫做共线向量 0 与任一向量 或共线 相等向量 长度 且方向 的向量 两向量只有相等或不等,不能比较大小 相反向量 长度 且方向 的向量 0 的相反向量为 0 零 相同 相反 方向相同或相反 平行 相等 相同 相等 相反 1 个单位 2.向量的线性运算 向量运算 定义 法则(或几何 意义) 运算律 加法 求两个向量和的运算 (1)交换律: a+b=b+a. (2)结合律: (a+b)+c=a+(b+c). 减法 求a与b的相反向量-b的和的运算叫做a与b的差 法则 a-b=a+(-b) 三角形三角形平行四边形 数乘 求实数 λ与向量 a的积的运算 (1)|λa|=|λ||a|. (2)当 λ>0 时,λa 的方向与 a 的方向 ; 当 λ<0 时,λa 的方向与 a 的方向 ;当λ=0 时,λa=0. λ(μa)=λμa; (λ+μ)a=λa+μa; λ(a+b)=λa+λb. 3.共线向量定理 向量 a(a≠0)与 b 共线的 条件是存在唯一一个实数 λ, 使得 b=λa. 相同 相反 充要 [难点正本 疑点清源] 1.向量的两要素 向量具有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的位置没有关系.同向且等长的有向线段都表示同一向量.或者说长度相等、方向相同的向量是相等的.向量只有相等或不等,而没有谁大谁小之说,即向量不能比较大小. 2.向量平行与直线平行的区别 向量平行包括向量共线(或重合)的情况,而直线平行不包括共线的情况.因而要利用向量平行证明向量所在直线平行,必须说明这两条直线不重合. 基础自测 1.化简OP→ -QP→ +MS→ -MQ→ 的结果等于________. 解析 OP→ -QP→ +MS→ -MQ→ =OP→ +PQ→ -(SM→ +MQ→ ) =OQ→ -SQ→=OQ→ +QS→=OS→. OS→ 2.下列命题:①平行向量一定相等;②不相等的向量一定 不平行;③平行于同一个向量的两个向量是共线向量; ④相等向量一定共线.其中不正确命题的序号是_______. 解析 ①错,如单位向量与 0 不相等;②错...