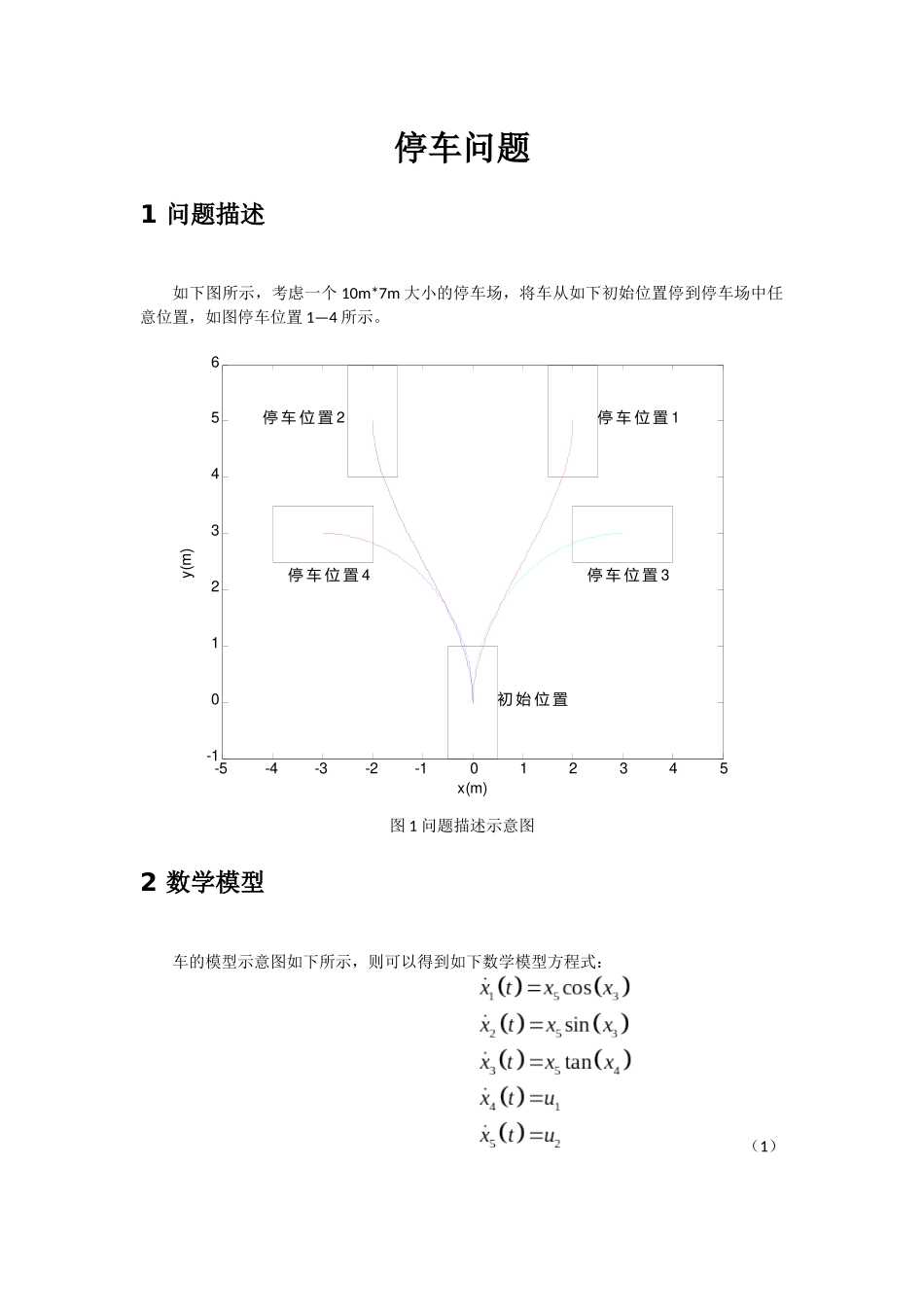
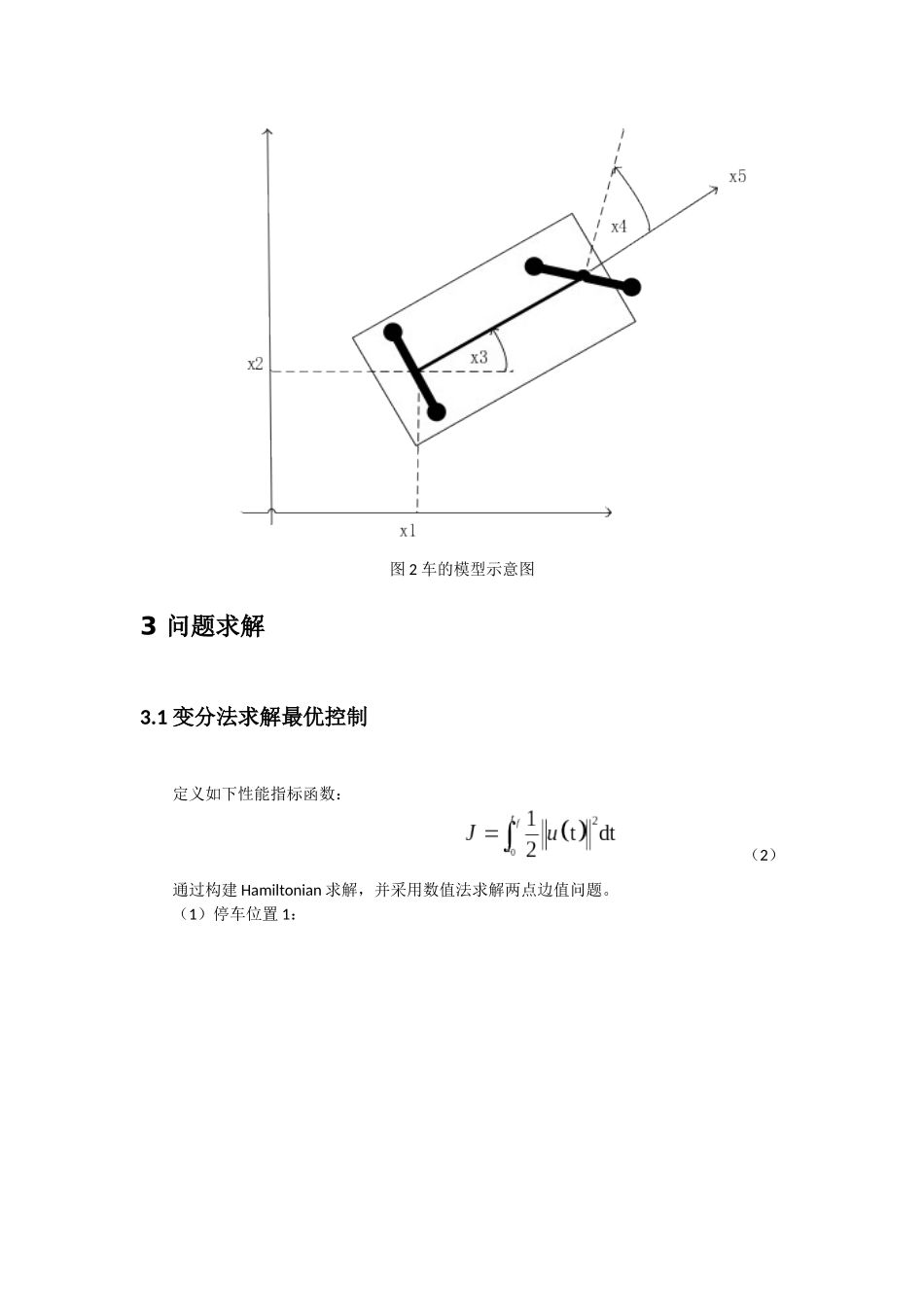
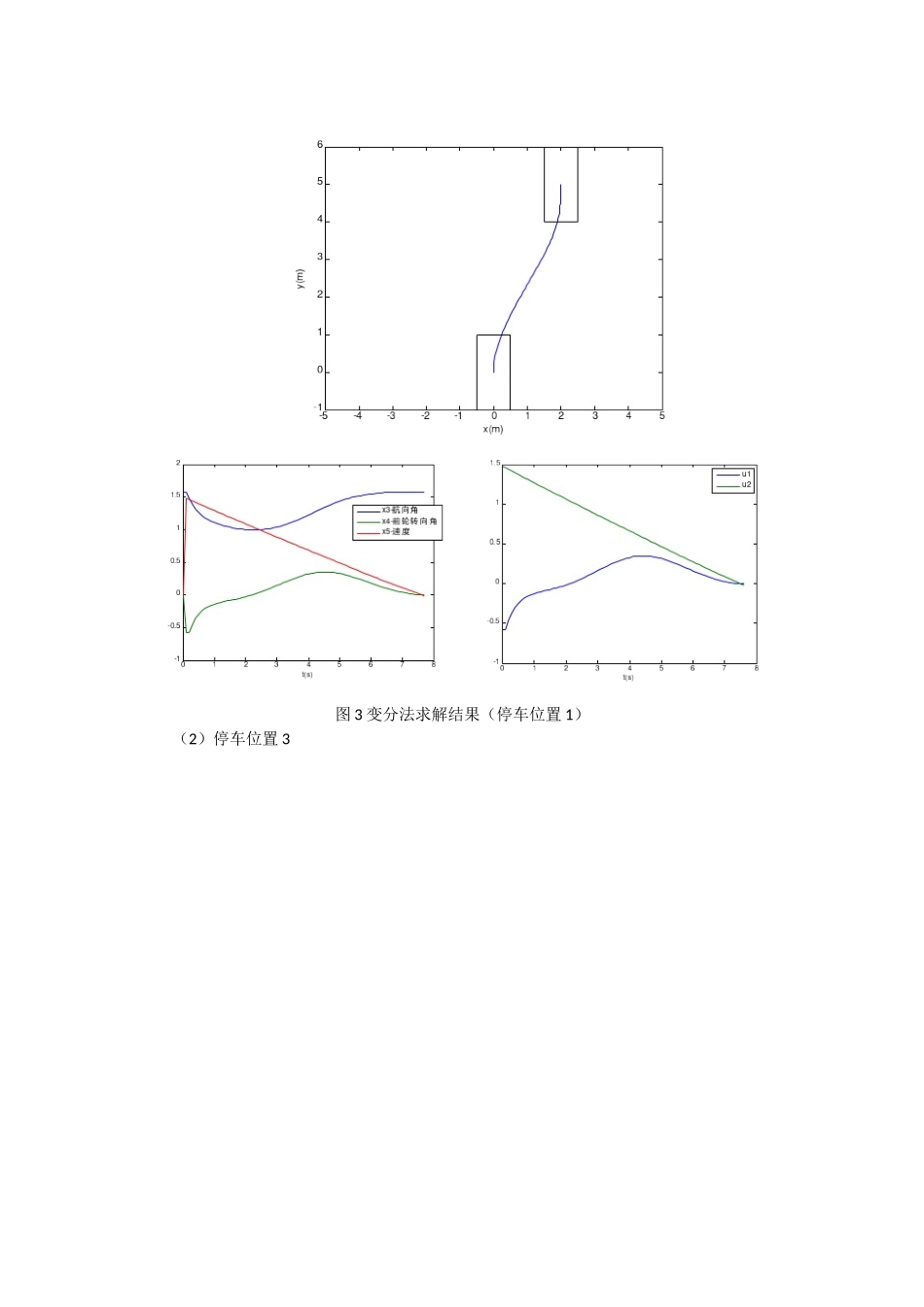
停车问题1 问题描述如下图所示,考虑一个 10m*7m 大小的停车场,将车从如下初始位置停到停车场中任意位置,如图停车位置 1—4 所示。-5-4-3-2-1012345-10123456初 始 位 置1停 车 位 置2停 车 位 置3停 车 位 置4停 车 位 置x(m)y(m)图 1 问题描述示意图2 数学模型车的模型示意图如下所示,则可以得到如下数学模型方程式: (1)图 2 车的模型示意图3 问题求解3.1 变分法求解最优控制定义如下性能指标函数: (2)通过构建 Hamiltonian 求解,并采用数值法求解两点边值问题。(1)停车位置 1:图 3 变分法求解结果(停车位置 1)(2)停车位置 3图 4 变分法求解结果(停车位置 3)3.2 动态规划法求解最优控制定义如下性能指标函数: (3)采用离散动态规划求解,分别将时间、状态量、控制量、状态方程和性能指标函数离散化。分别尝试不同的离散化程度。(1)第一次离散化求解:运行时间(1120s)离散化后的维度为:时间(150);状态(4*10*2*3*6);控制(6*6)图 5 动态规划求解结果(第一次离散化)(2)第二次离散化求解: 运行时间(70291s)离散化后的维度为:时间(30);状态(10*25*12*16*15);控制(15*15)图 6 动态规划求解结果(第二次离散化)3.3 直接打靶法求解最优控制定义如下性能指标函数: (4)采用 SQP 方法求解,结果如下:(1)停车位置 1图 7 直接打靶法求解结果(停车位置 1)(2)停车位置 3图 8 直接打靶法求解结果(停车位置 3)3.4 模型预测控制求解最优控制定义如下性能指标函数:(5)预测步长 ,控制步长。(1)停车位置 1图 9 模型预测控制求解结果(停车位置 1)(2)停车位置 3图 10 模型预测控制求解结果(停车位置 3)3.5 自适应动态规划求解最优控制(尝试)首先采用经典的 HDP92 方法进行尝试,但多次试验的效果都不好;之后尝试每次用数值法求解最优的控制量,但效果依旧很差;然后采用值迭代的方法,并尝试用二次型近似值函数和神经网络近似值函数两种方式,但是最后的效果依旧很差(包括一般值迭代和广义值迭代)。(上述方法对 PPT 上的例子,效果还不错)4 结果分析变分法求解最优控制:针对本问题这样一个相对复杂的模型,变分法无法很好地处理控制量和状态量的约束。而且在求解过程中,由于无法得到解析解,因而需要采用数值法求解一个两点边值问题。而在采用 BVP4C 求解时,需要经过多次初值选择试凑,才能保证可解...