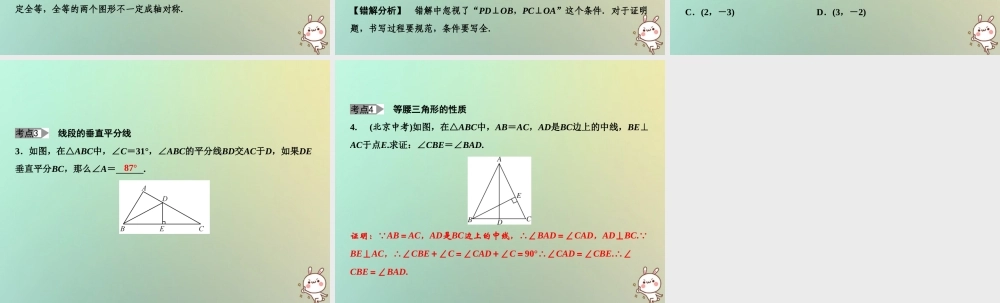
第 15 章 轴对称图形与等腰三角形 章末小结 2018 秋季数学 八年级 上册 • HK 【易错分析】 易错点1:混淆轴对称和轴对称图形 轴对称和轴对称图形是两个不同的概念,它们虽然都具有对称的关系,但轴对称是针对两个图形而言的,而轴对称图形指的是一个图形. 【例1】对于右图中的“雪花折线图”,小新说它成轴对称,这种说法可以吗? 【错解】 可以. 【正解】 不可以. 【错解分析】 如果把整个图形看作由两个相同的部分组成的两个图形,那么就可以说这“两部分图形”成轴对称.但对于整个图形,说它是成轴对称就错了.正确的说法是:图中的图形是轴对称图形. 易错点2:没有真正理解轴对称的概念 两个全等的图形成轴对称还要满足一定的位置关系,即找到一条直线,把一个图形沿着这条直线折叠,使它能够与另一个图形重合. 【例2】如果两个图形的大小、形状完全一样,放在一起能够完全重合,那么这两个图形一定关于某条直线成轴对称,这种说法是否正确? 【错解】 正确. 【正解】 不正确. 【错解分析】 错解没有真正理解轴对称的概念,成轴对称的两个图形一定全等,全等的两个图形不一定成轴对称. 易错点3:证明过程中漏条件而出错 【例3】如图所示,点P在∠AOB的平分线上,且PD⊥OB,PC⊥OA,垂足分别为D、C.求证:PD=PC. 【错解】 ∵点P在∠AOB的平分线上,∴PD=PC. 【正解】 ∵点P在∠AOB的平分线上,PD⊥OB,PC⊥OA,∴PD=PC. 【错解分析】 错解中忽视了“PD⊥OB,PC⊥OA”这个条件.对于证明题,书写过程要规范,条件要写全. 【考点分类训练】 轴对称图形的识别 1.下列图形中是轴对称图形的是( ) 轴对称与图形的坐标 2.在平面直角坐标系中,点 P(-3,2)关于直线y=x对称点的坐标是( ) A.(-3,-2) B.(3,2) C.(2,-3) D.(3,-2) A C 线段的垂直平分线 3.如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于D,如果DE垂直平分BC,那么∠A= . 87° 等腰三角形的性质 4. (北京中考)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD. 证明:∵AB=AC,AD是BC边上的中线,∴∠BAD=∠CAD,AD⊥BC.∵BE⊥AC,∴∠CBE+∠C=∠CAD+∠C=90°∴∠CAD=∠CBE.∴∠CBE=∠BAD.