等差数列的前n项和 新课标 人教版 课件VIP免费

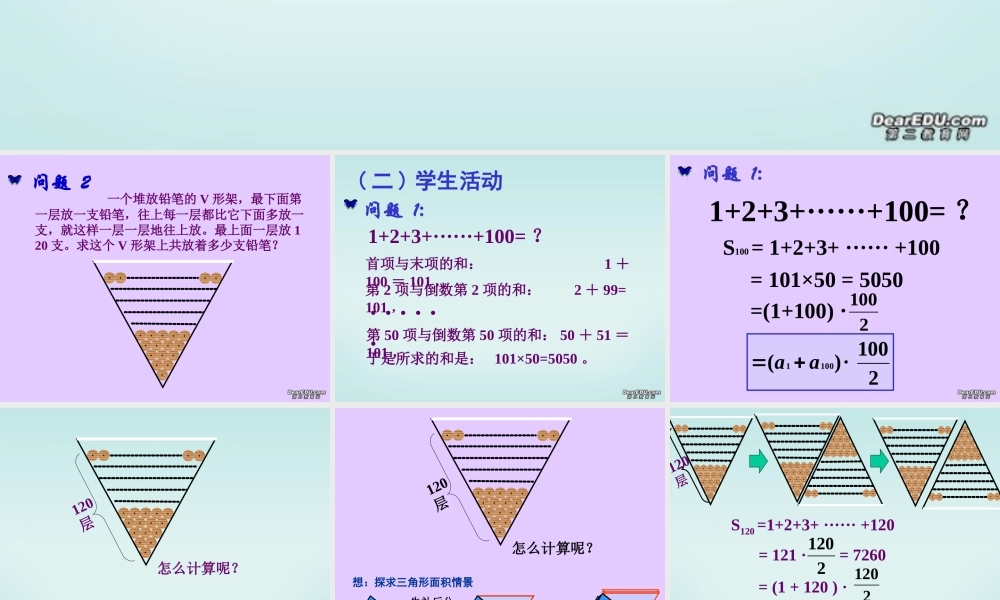
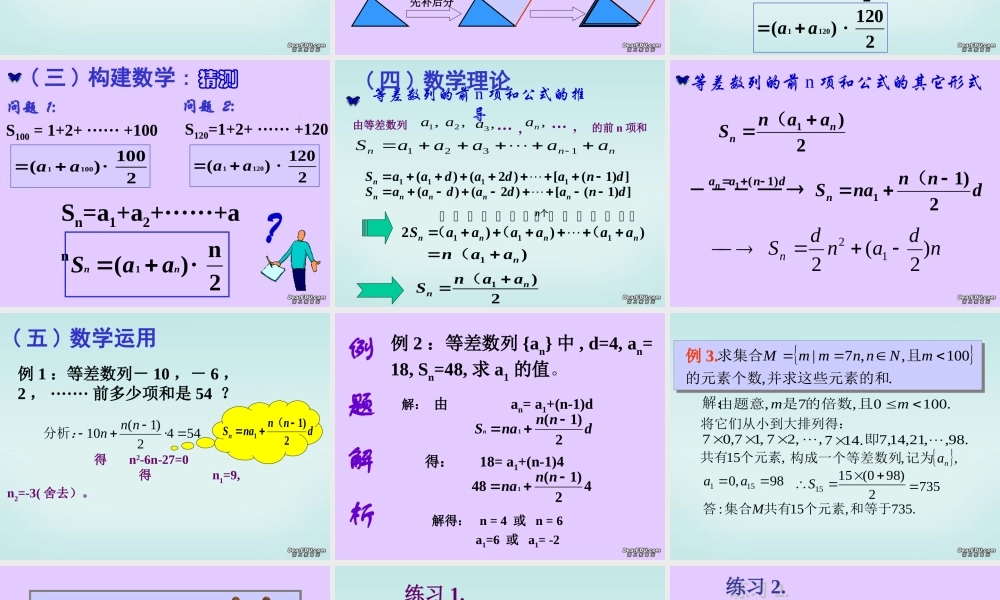
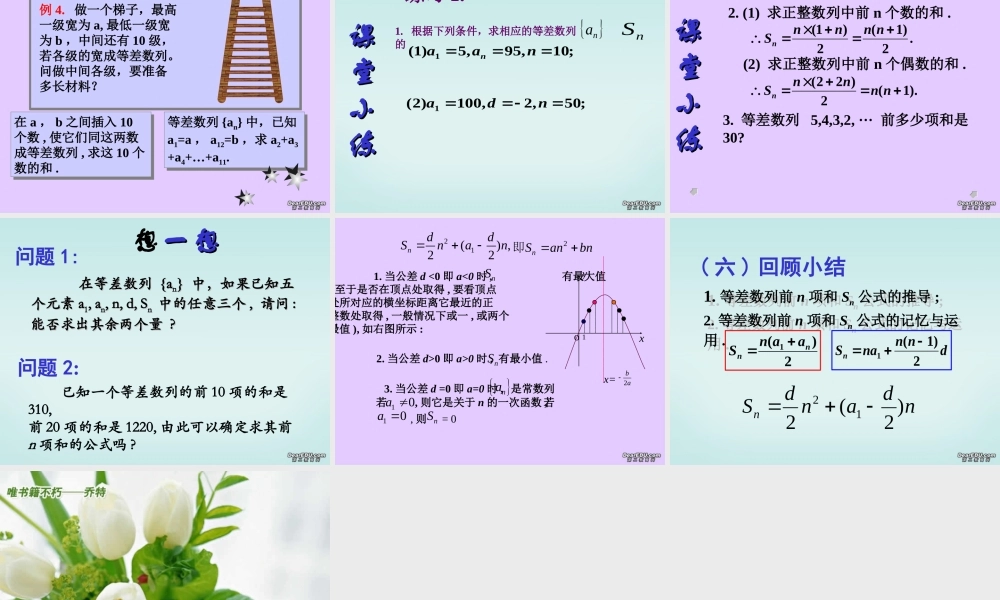
问题 1:1+2+3+······+100= ？案例 1 等差数列前n 项和( 一 ) 问题情景问题 2 一个堆放铅笔的 V 形架，最下面第一层放一支铅笔，往上每一层都比它下面多放一支，就这样一层一层地往上放。最上面一层放 120 支。求这个 V 形架上共放着多少支铅笔？问题 1:1+2+3+······+100= ？首项与末项的和： 1 ＋100 ＝ 101 ，第 2 项与倒数第 2 项的和： 2 ＋ 99=101 ， · · · · · · 第 50 项与倒数第 50 项的和： 50 ＋ 51 ＝101 ，于是所求的和是： 101×50=5050 。( 二 ) 学生活动S100 = 1+2+3+ ······ +100=(1+100) · 21002100· )(1001aa 问题 1:1+2+3+······+100= ？= 101×50 = 5050120层怎么计算呢？120层怎么计算呢？先补后分想：探求三角形面积情景120层 = 121 · = 72602120= (1 + 120 ) · 21202120· )(1201aa S120 =1+2+3+ ······ +120问题 1:S100 = 1+2+ ······ +1002100· )(1001aa 问题 2:S120=1+2+ ······ +1202120· )(1201aa 2n· )(1nnaaSSn=a1+a2+······+an?( 三 ) 构建数学 : 猜测等差数列的前 n 项和公式的推导,1a,2a,3a,na… ，… ，nnnaaaaaS 1321由等差数列的前 n 项和])1([)2()(1111dnadadaaSn])1([)2()(dnadadaaSnnnnn个（（（nnnnnaaaaaaS)))2111)1naan （2)1nnaanS （( 四 ) 数学理论等差数列的前 n 项和公式的其它形式2)1nnaanS （dnaan)1(1dnnnaSn2)11（ndandSn)2(212例 1 ：等差数列－ 10 ，－ 6 ，2 ， ······· 前多少项和是 54 ？dnnnaSn2)11（ 得 n2-6n-27=0 得 n1=9, n2=-3( 舍去）。 544· 2)1(10nnn：分析( 五 ) 数学运用例题解析例 2 ：等差数列 {an} 中 , d=4, an=18, Sn=48, 求 a1 的值。dnnnaSn2)1( 1解： 由 an= a1+(n-1)d得： 18= a1+(n-1)442)1(84 1nnna解得： n = 4 或 n = 6a1=6 或 a1= -2 .,100,,7| 并求这些元素的和的元素个数且求集合mNnnmmM.,100,,7| 并求这些元素的和的元素个数且求集合mNnnmmM例 3.例 3.解：.1000,7,...