一、复习回顾: 1 、对数的概念:2 、指数函数的定义 :如果 a b ═N ,那么数 b 叫做以 a 为底 N 的对数,记作 log a N = b ( a>0,a≠1 ) 函数 y = ax ( a > 0, 且 a ≠ 1 ) 叫做指数函数 , 其中x 是自变量 . 函数的定义域是 R.问题 :求指数函数 y = ax ( a > 0 , 且 a ≠ 1 ) 的反函数解: 从 y = ax 可以解得: x = logay 因此指数函数 y = ax 的反函数是 y = logax ( a > 0 , 且 a ≠ 1 ) 又因为 y = ax 的值域为( 0 ,+∞) 所以 y = logax ( a > 0 , 且 a ≠ 1 ) 的定义域为( 0 ,+∞)一般地 函数 y = logax (a > 0, 且 a≠1) 是指数函数 y = ax 的反函数函数 y = loga x (a > 0, 且 a≠ 1 ) 叫做对数函数 . 其中 x 是自变量 , 函数的定义域是( 0 , +∞ )对数函数和指数函数 互为反函数对数函数的定义:y = xy = 2xy = log2x 1 2 3 4 5 6 7 8yx08 7654321-3 -2 -1-1-2-3 2 、描点作出 的图象;3、作直线 y=x ;4、描出关于 y=x 的对称点;y = 2x5、用平滑曲线连结所得的点。作图过程1 、建立直角坐标系;作出函数 y = log 2 x 的图象 1 2 3 4 5 6 7 8yx08 7654321-3 -2 -1-1-2-30.5logxy=的函数图象也可以直接描点作出x0.1250.251248y320-1-2-31 、列表2、建立直角坐标系3、描点4、用平滑曲线连结各点x21logy=xy01y = log2xy=log 0.5 x 图象特征 函数性质 图像都在 y 轴右侧图像都经过 (1,0) 点 1 的对数是 0㈠㈡当底数 a > 1 时 ; x > 1 , 则 logax > 0 0 < x < 1 , 则 logax < 0当底数 0 < a < 1 时 ; x > 1 , 则 logax < 0 0 < x < 1 , 则 logax > 0图像㈠在 (1,0) 点右边的纵坐标都大于 0, 在 (1,0) 点左边的纵坐标都小于 0;图像㈡则正好相反自左向右看 , 图像㈠逐渐上升 图像㈡逐渐下降当 a > 1 时 ,y = logax 在 (0,+∞) 是增函数当 0 < a < 1 时 ,y = logax 在 (0,+∞) 是减函数定义域是 ( 0, +∞)图象a>10
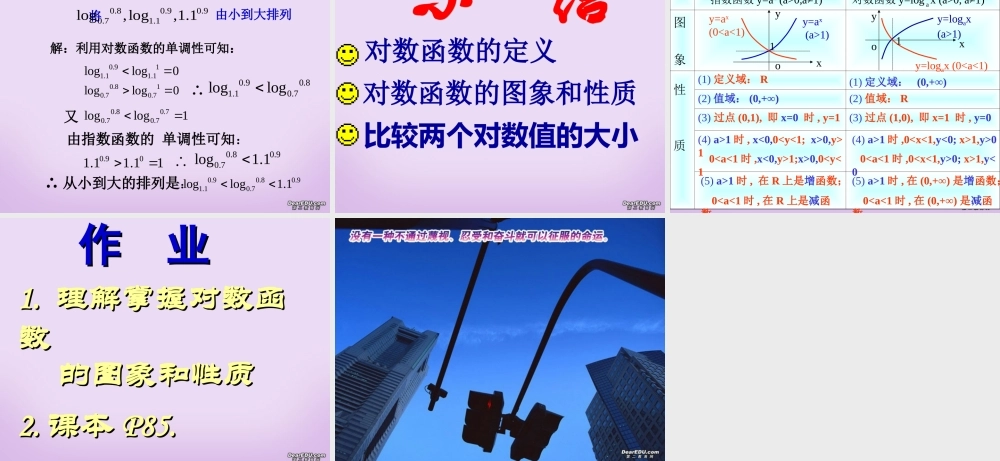
0, a≠1)(4) 01 时 , y>0(4) 00; x>1 时 , y<0 (3) 过点 (1,0), 即 x=1...