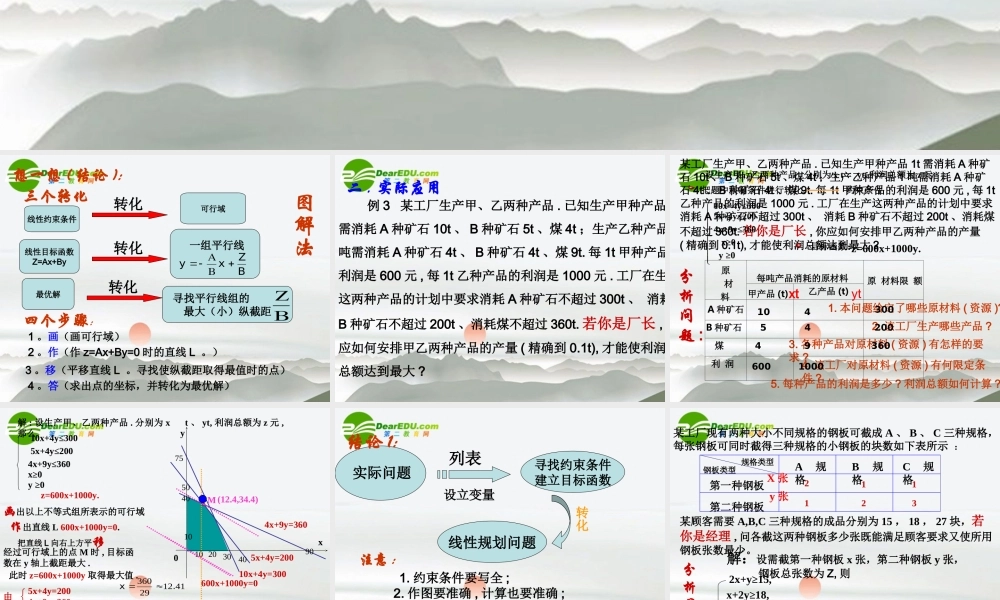
简单的线性规划( 第 3 课时 )转化转化转化四个步骤:1 。画(画可行域)三个转化4 。答(求出点的坐标,并转化为最优解)3 。移(平移直线 L 。寻找使纵截距取得最值时的点)2 。作(作 z=Ax+By=0 时的直线 L 。)图解法想一想 ( 结论 ):线性约束条件可行域线性目标函数Z=Ax+By一组平行线BZxy最优解寻找平行线组的 最大(小)纵截距 例 3 某工厂生产甲、乙两种产品 . 已知生产甲种产品 1t需消耗 A 种矿石 10t 、 B 种矿石 5t 、煤 4t ;生产乙种产品 1吨需消耗 A 种矿石 4t 、 B 种矿石 4t 、煤 9t. 每 1t 甲种产品的利润是 600 元 , 每 1t 乙种产品的利润是 1000 元 . 工厂在生产这两种产品的计划中要求消耗 A 种矿石不超过 300t 、 消耗B 种矿石不超过 200t 、消耗煤不超过 360t. 若你是厂长 , 你应如何安排甲乙两种产品的产量 ( 精确到 0.1t), 才能使利润总额达到最大 ?二 . 实际应用某工厂生产甲、乙两种产品 . 已知生产甲种产品 1t 需消耗 A 种矿石 10t 、 B 种矿石 5t 、煤 4t ;生产乙种产品 1 吨需消耗 A 种矿石 4t 、 B 种矿石 4t 、煤 9t. 每 1t 甲种产品的利润是 600 元 , 每 1t乙种产品的利润是 1000 元 . 工厂在生产这两种产品的计划中要求消耗 A 种矿石不超过 300t 、 消耗 B 种矿石不超过 200t 、消耗煤不超过 360t. 若你是厂长 , 你应如何安排甲乙两种产品的产量( 精确到 0.1t), 才能使利润总额达到最大 ?分析问题 :1. 本问题给定了哪些原材料 ( 资源 )?2. 该工厂生产哪些产品 ?3. 各种产品对原材料 ( 资源 ) 有怎样的要求 ?4. 该工厂对原材料 ( 资源 ) 有何限定条件 ?5. 每种产品的利润是多少 ? 利润总额如何计算 ? 原 材料每吨产品消耗的原材料A 种矿石B 种矿石煤甲产品 (t)乙产品 (t)1054449原 材料限 额300200360利 润6001000xtyt把题中限制条件进行转化:约束条件10x+4y≤3005x+4y≤2004x+9y≤360x≥0y ≥0z=600x+1000y. 目标函数:设生产甲、乙两种产品 . 分别为 x t 、 yt, 利润总额为 z 元解 : 设生产甲、乙两种产品 . 分别为 x t 、 yt, 利润总额为 z 元 ,那么10x+4y≤3005x+4y≤2004x+9y≤360x≥0y ≥0z=600x+1000y.画出以上不等式组所表示的可行域作出直线 L 600x+1000y=0.解得交点...